Conflict in a "ladder" problem

Question

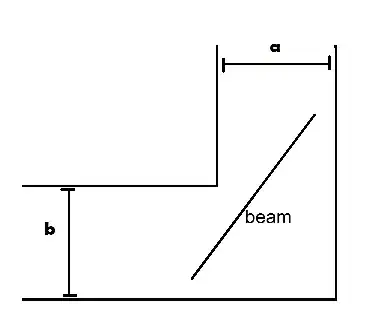
The problem that I want to talk about is this: find the length of the longest beam (width = 0) that can be moved horizontally from a corridor of width $a$ into a corridor of width $b$. If the two corridors are perpendicular to each other.

Sketch of the situation:

Most of you have seen this.

My problem is not HOW to get the answer, but my problem is that I don't actually understand why the answer is in fact the answer we want.

To get the answer we looked for when the beam can get stuck, and we calculated the shortest beam that will get stuck and we concluded "The shortest beam that can get stuck is the longest beam that can get carried in the corridors."

THAT is my problem: why is the shortest beam that can get STUCK the longest beam that can get carried in the corridors? (This should be the title, but this was too long I thought)

What I thought of:

If we say $\mathcal{L} \in \mathbb{R}$ is the shortest length of the beam that can get stuck, then the longest beam must be smaller than $\mathcal{L}$. But we can't find the longest, because we can always find a longer beam that is smaller than $\mathcal{L}$. So, we will take the supremum of all beams with length $l$ that won't get stuck: $\underset{l<\mathcal{L}}{\sup} \{l\} = \mathcal{L}$.

So, is that the reason why we say that the longest beam is $\mathcal{L}$? If not, what is the reason then?

Answer 1

The way I view the problem is, if we want to move a beam of length $k$, where $k < \mathcal L$, around the corner, we can place the beam against the outside wall of the corridor we are moving from, slide it until one end of the beam touches the outside wall of the corridor we are moving to, then slide that end of the beam along the "to" wall while keeping the other end on the "from" wall. The beam will never touch the inside corner where the two corridors meet, so we are able to move it completely around the corner.

If we take a beam of length $m > \mathcal L$, however, and try the maneuver described above, at some point the beam will touch the inside corner and not be able to move any farther, because to keep both ends on the two walls as we did with the shorter beam, the longer beam would have to cut through the walls on the inside corner.

The question is, what happens if, while maneuvering the beam as described, the beam just barely touches the inside corner but never needs to cut through it. (That is what happens when the length is exactly $\mathcal L$.) Does that beam get stuck, or does it pass around the corner?

My interpretation in the past has been that the beam passes around the corner as long as we can slide the beam along the outside walls while keeping all other points of the beam inside or on the walls of the corridors. That is, it is OK to touch the inside corner, but not to cut through the walls at that corner. So I would say that the beam of length $\mathcal L$ is precisely the length of the longest beam that can pass around the corner horizontally (not a supremum). Under that interpretation, of course, there is no beam that gets stuck and is shorter than all other beams that get stuck, so I would interpret "the shortest beam that gets stuck" to be an abbreviated, informal way of describing the infimum of the lengths of all beams that get stuck.

Your interpretation works too; it just takes the "shortest" description literally and interprets the "longest" description as having been somewhat informal.

In the last analysis, either a beam of length exactly $\mathcal L$ gets stuck or it doesn't; one of the two phrases "longest that passes through" or "shortest that gets stuck" will have to be reinterpreted as a bound that is not actually achieved. I prefer that the intermediate step of the solution, not the initial problem statement, is the one to be reinterpreted, but that may be a matter of taste.