How to determine the outcome of the recursive sequence $a_n=\frac{1}{\operatorname{abs}\left(a_{n-1}\right)-1}$

Question

Depending on the starting value, the end result of this iterative sequence appears to be very variable, for example, if the starting value $a_0\ =\frac{b}{c}$ where $b$ and $c$ are integers, then eventually the sequence appears to always reach 0, and then infinity afterwards, ending the sequence.

Another situation is if the starting value is in the form $\frac{b+\sqrt{5}}{2}$ where $b$ is an integer, this now appears to converge to either $\frac{1+\sqrt{5}}{2}$ or ends up switching between $\frac{1-\sqrt{5}}{2}$ and $\frac{-3-\sqrt{5}}{2}$ endlessly.

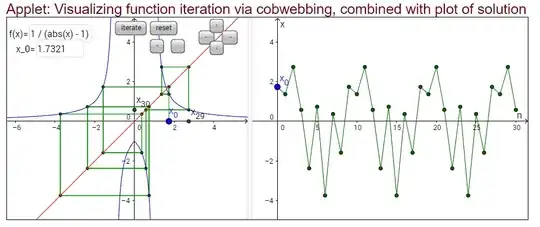
Yet again another situation, where the starting value is not rational and not in the form I described previously, sometimes other starting values experience periodicity e.g. for $a_0 = \sqrt{3}$ there are only 9 values that the sequence can take. Also similar to this category, some values are not initially periodic but eventually hit a value which is; e.g. $a_0 = 3-\sqrt{3}$ .

Outside of these categories, there are some which I imagine should never converge e.g. $\pi$ , although it does have a tendency to tend towards $-1$ and then towards a very large number, before cycling back to a small one again.

EDIT: this is an interesting visualisation for the $\sqrt{3}$ case (see figure 1)

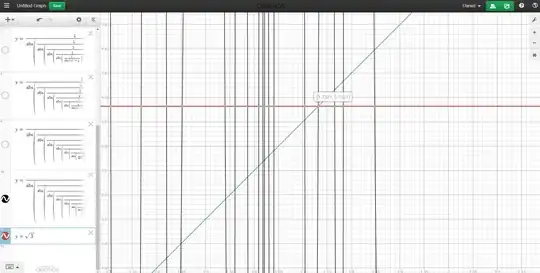
EDIT 2: this is another interesting discovery, if i put $f(x)=x$ for n iterations in a graphing calculator and record all of the points where the graph $y=x$ intersects the other graph, all of these points are the values of $x_0$ which are periodic of period n (see figure 3, i have written the equation for 9 iterations and found a fixed point at $\sqrt{3}$).

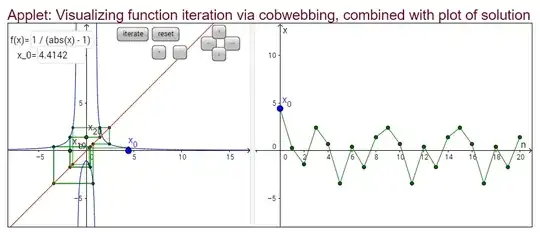
I also notice that the number of fixed points appears to be getting much larger each time, and these fixed points are particularly dense around the golden ratio phi and this might indicate that after an arbitrarily large number of iterations, we have an arbitrarily large number of fixed points, though I don't know if this would cover all algebraic numbers . However, some other values for $x_0$ may not themselves be periodic, but eventually reach one that is e.g. $3+\sqrt{2}$ (see figure 2)

(figure 1)

(figure 2)

(figure 3)

My question is, can it be

a.) Proven/disproven that for starting value a/b , the sequence will eventually reach 0?

b.) Proven/disproven that for any algebraic number, the sequence is eventually finitely periodic, and if so, is there are a way of determining its period?

c.) Proven/disproven that the sequence does not converge for transcendental numbers?

Any information on this topic would be greatly appreciated!

Answer 1

Since the iterating map $f : a \mapsto \frac 1 {|a|-1}$ is a piecewise rational homography, and because rational homographies are a group under composition, any iterate of $f$ is again a piecewise rational homography.

Then, cycles can only occur at a fixpoint of one of those homographies, and their fixpoints are quadratic numbers : if $x = \frac {ax+b}{cx+d}$ for rational $a,b,c,d$, then $cx^2+(d-a)x-b = 0$, which is a quadratic equation in $x$ with rational coefficients.

---

We can count the number of cycles for each $n$, and also see what possible sequence of sign you can get.

Split the circle $\Bbb R \cup \{\infty\}$ into four parts $A=[\infty ; -1],B=[-1;0],C=[0;1],D=[1;\infty]$. $f$ sends $A$ and $D$ on $C \cup D$, and sends $B$ and $C$ on $A$.

With this we can quickly determine by induction that if $F_0 = 0, F_1 = 1, \ldots$ is the Fibonacci sequence,
$f^{\circ n}$ sends $A$ and $D$ on ($F_{n-1}$ times $A$ and $F_n$ times $C$ and $D$) ; and it sends $B$ and $C$ on ($F_{n-2}$ times $A$ and $F_{n-1}$ times $C$ and $D$).

Each time you have a piece of $f^{\circ n}$ sending a subinterval of $A$ onto a whole $A$, you get exactly one fixpoint in that interval, and the same goes for $B,C,D$.
This gives you $F_{n-1} + F_{n-1} + F_n$ fixpoints in total for every piece of $f^{\circ n}$. That's the Fibonacci-like sequence $1,3,4,7,11,18,\ldots$

(except for the cycle $0 \mapsto -1 \mapsto \infty \mapsto 0$, they all have to be inside the intervals so they are only counted once. But so is this one because we only count the "half" of $0$ that occurs in $C$)

By looking at that Fibonacci-like sequence then removing the smaller cycles coming from divisors of $n$, you get $1,1,1,1,2,2,\ldots$ cycles of length exactly $1,2,3,4,5,6\ldots$

Moreover, a number is completely determined by which intervals $C,A,D$ the sequence goes through. Any $C$ is followed by a $A$, while $A$ or $D$ can be followed by $C$ or $D$.

Going back to signs, knowing the sequence of intervals is the same as knowing the sequence of signs. A negative sign correspond to a $C$, a positive sign correspond to $C$ or $D$ according to if the next sign is positive or not, so the possible sign sequences are every possible sequence where there is no consecutive $-$ sign, and again, an irrational number is completely determined by the sequence of signs it goes through

If you are on a positive real, then you will see a bunch of $CA (+-)$ and $D (+)$, and of course, numbers that are on cycles correspond to periodic sequences.

For example the $4$-cycle correspond to repeating $CADD (+-++)$ and two $5$-cycles correspond to $CACAD (+-+-+)$ and $CADDD (+-+++)$

---

If you know about continued fractions, they come from a similar piecewise homography $g$ on positive real numbers ($g(x) = x-1$ if $x \ge 1$ and $g(x) = \frac 1x$ if $0 < x \le 1$).

In fact, they are very much intertwined.
If $2 \le x$ then $f(x) = \frac 1{x-1} > 0$, $f(f(x)) = \frac{1-x}{x-2} < 0$, and $f(f(f(x))) = x-2 = g(g(x))$

If $1 \le x \le 2$ then $f(x) = \frac 1{x-1} = g(g(x))$

If $0 \le x \le 1$ then $f(x) = \frac {-1}{1-x} < 0$, $f(f(x)) = \frac{1-x}x = \frac 1x - 1 = g(g(x))$

So iterating $f$ on some number will reach (among others), all the iterates of $g\circ g$ on that number.

In particular, if you start on a positive real, you reach large a number if and only if you reach a large number when computing the continued fraction of that real (that's what you see happening with $\pi$ for example)

In particular, any quadratic number has a continued fraction which is eventually periodic, so under your iteration, their trajectory will be eventually periodic as well : quadratic numbers correspond exactly to eventually periodic sign sequences.

Answer 2

First of all, let me change your problem statement from $\displaystyle a_{n+1}={1\over|a_n|-1}$ to $\displaystyle a_{n+1}={1\over|a_n-1|}$. It is equivalent in anything but the sign (that is, if $a_0>0$), and will let us stay conveniently on the positive half-line.

Now suppose we have a rational number $a_1={p\over q}$. Let's define a norm: $\max(p,q)$. What will become of it? There are two distinct cases:

$$\begin{align}a_1>1\;\Rightarrow\;p>q\;\Rightarrow\;\; a_2={q\over p-q}\\ a_1<1\;\Rightarrow\;p<q\;\Rightarrow\;\; a_2={q\over q-p} \end{align}$$ So the norm strictly decreases after any term which is greater than 1, and does not change after a term which is less than 1. Note that a term less than 1 is always immediately followed by a term greater than 1 (the reverse is not true), so making two steps is guaranteed to decrease the norm. Note also that there are only so many rational numbers with given norm, so this descent can't be infinite; it must end somewhere, and we seem to know where.

Now let's deal with the periodic points. $f(x)$ is piecewise linear-fractional, hence so are all its iterations. In other words, $f(f(\dots(x)\dots))$ is essentially $ax+b\over cx+d$, only its domain consists of multiple intervals, and the coefficients depend on the interval. Well, but then equating this to $x$ is equivalent to a quadratic equation (or rather a bunch thereof, one for each interval), and their roots, however many, are all quadratic irrationalities. That's it; there can be no other periodic points. Even the algebraic numbers of higher degree won't do.

I don't quite see why all quadratic irrationalities must eventually converge to some cycle, but it seems they do. Let's think of it later.

Answer 3

Not a complete answer, given integers are a particular case of $\frac{a}{b}$ let's look at the following case, $n \in \mathbb{N}, n > 2$, then $x_0=n \rightarrow \frac{1}{n-1} \rightarrow \frac{1}{\frac{1}{n-1}-1}=\frac{n-1}{2-n}\rightarrow \frac{1}{\left|\frac{n-1}{2-n}\right|-1}=n-2$. Similar fate will have a starting point $x_0=-n$. So

• if we start with an even $2p$ after $3$ iterations $\rightarrow 2(p-1)$, after $3$ iterations $\rightarrow 2(p-2)$ ... $\rightarrow 2 \rightarrow 1\rightarrow \infty$
• if we start with an odd $2p+1$ after $3$ iterations $\rightarrow 2(p-1)+1$, after $3$ iterations $\rightarrow 2(p-2)+1$ ... $\rightarrow 3 \rightarrow \frac{1}{2} \rightarrow -2 \rightarrow 1 \rightarrow \infty$

Integers end up at infinity. Arguably, we could say that the next iteration will throw them at $0$, but I think it's a speculation, thus this should qualify as a counter-example for a)

Other than that, I agree with @mercio regarding the similarity with continued fractions. Imagine $$\alpha=a_0+\frac{1}{a_1+\frac{1}{a_2+...}}=a_0+\frac{1}{\beta}$$

• if $a_0=2p+1$, $\alpha \rightarrow$ after $3$ iterations $\alpha-2=a_0-2+\frac{1}{\beta} \rightarrow $ ... $\rightarrow 3+\frac{1}{\beta} \rightarrow \frac{1}{2+\frac{1}{\beta}}\rightarrow \frac{1}{\frac{1}{2+\frac{1}{\beta}}-1}=\frac{2+\frac{1}{\beta}}{-1-\frac{1}{\beta}}\rightarrow \frac{1}{\frac{2+\frac{1}{\beta}}{1+\frac{1}{\beta}}-1}=1+\frac{1}{\beta}\rightarrow \frac{1}{1+\frac{1}{\beta}-1}=\beta=a_1+\frac{1}{a_2+...}$
• if $a_0=2p$, $\alpha \rightarrow$ after $3$ iterations $\alpha-2=a_0-2+\frac{1}{\beta} \rightarrow $ ... $\rightarrow 2+\frac{1}{\beta} \rightarrow \frac{1}{1+\frac{1}{\beta}}\rightarrow$ $\frac{1}{\frac{1}{1+\frac{1}{\beta}}-1}=\frac{1+\frac{1}{\beta}}{-\frac{1}{\beta}}=-\beta-1\rightarrow \frac{1}{\beta+1-1} \rightarrow$ $\frac{1}{\frac{1}{\beta}-1}=\frac{\beta}{1-\beta} \rightarrow \frac{1}{\frac{\beta}{\beta-1}-1}=\beta-1=a_1-1+\frac{1}{a_2+...}$, this is of course assuming $a_1>0$.

Then there is this book by Khinchin which states that "any quadratic irrational number has a periodic continued fraction" as Theorem 28.