A beautiful fact is that
The space of configurations of a 5-vertex polygon with unit length sides, two of whose vertices are fixed, is a closed orientable surface of genus $3$.
Similarly, but much more simply, the torus is the space of configurations of a double pendulum.
Are there other natural realizations of high genus closed orientable surfaces?
Actually, there are several relatively simple planar linkages whose configuration spaces are surfaces of higher genera. For instance, if $S_n$ is a linkage which is a "spider" with $n$ legs each of which has one joint and such that tips of the legs are glued to the plane, then the configuration space of $S_n$ is a surface of certain genus $g$. Such linkages (with $n=3$) first were analyzed (to the best of my knowledge) in a paper by Thurston and Weeks:
W. Thurston and J. Weeks, The Mathematics of three dimensional manifolds, Scientific American, 251 (1984) 94-106.
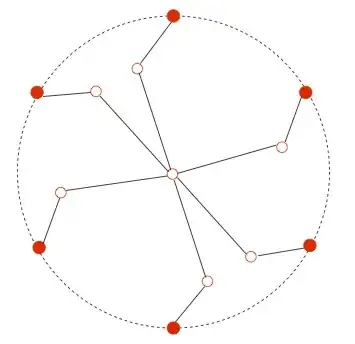
The following is a theorem proven in
P.Mounoud, Sur l’espace des configurations d’une araignee. Osaka J. Math., 48(1):149–178, 2011.
Theorem. Let $g$ be an natural number and $r$ the biggest integer such that $2r$ divides $g-1$. A compact orientable surface of genus $g$ is diffeomorphic to the configuration space of some spider if and only if $$ 2^{-r}(g − 1) \le 6r + 12.$$
On the other hand, if one allows linkages which are "centepides" then the oriented surface of any given genus is realized:
D. Jordan and M. Steiner Compact surfaces as configuration spaces of mechanical linkages, Israel Journal of Mathematics, 122 (2001) 175–187,
