So, on one hand you should clarify what does the sum() range over, but let's start with the transition function $T(s,a,s')$ : it's a function of three arguments; the future state $s'$, the action taken $a$ and the current state $s$.
Informally, $T$ records all the combinations of "where we are", "what action we take" and "where will we be next".
We know that both the state space and the action set are discrete (can be labeled as integer numbers) and rather small, so $T$ can be completely enumerated; it can be thought of as a table with $n_s \times n_a \times n_s$ entries.
However $T$ is also sparse (many, if not most, elements are $0$), since certain state jumps are not possible: in our gridworld example, one can only go from $a_3$ to either $a_2$ or $b_3$ (let's just number the states from 1 to 6 from now on and the actions U-L-D-R as 1 to 4), so $$T(s = 6,\cdot,\cdot) = \begin{array}{c} U \\L \\ D \\ R \end{array} \left( \begin{array}{c c c c c c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \mathbf{1} & 0 \\ 0 & 0 & \mathbf{1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right) $$
The other "slices" of $T$ correspond to the other 5 states.
The equation you wrote above models the value of being in the present state $s$. It should be written as $$U(s) = R(s) \, \gamma \max_i \left[ \sum_j T(s,a_i,s_j') U(s_j') \right]$$ so that we "marginalize out" the future state (by summing over $s_j'$) and then seek the action that maximizes that sum.
To emphasize: the value of any current state depends on the available choices and on the reward associated with each of those.
The above is only half of the story: the formula simply tells us the utility of every current state $U(s)$, but its definition is recursive: every action carries some consequences, and those in turn must be acted upon in order to maximize the total reward.
How do we actually compute it? We set an initial condition (the initial state $s_0 = 3$), as well as the known rewards $R(4) = -100$ and $R(2) = 10$, and $0$ elsewhere; compute $U$ for each possible action, and repeat (i.e set current state to $s_1$ and evaluate all possible $s_2$, etc. ) until we reach some desired final state $\hat{s}$ having $U(\hat{s}) = \max_s U(s)$.
At this point we backtrack, keeping note of which sequence of actions led to $\hat{s}$. This backward "integration" (if you think of the agent as a dynamical system literally moving through space) is the central principle of the Bellman equation (it's also called backward induction).
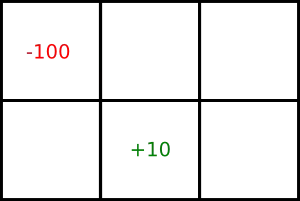
a3. An example would help me visualize it easily – Eka Oct 02 '16 at 17:06