prove that if n is an odd integer then n^2 has a remainder of 1 when divided by 8

Question

I am not sure how to prove that if $n$ is odd then the square of $n$ has a remainder of $1$ when divided by $8$.

Answer 1

Suppose $n$ is an odd integer. Then $n = 2k+1$ for some $k \in \mathbb{Z}$, and so $$n^2 = (2k+1)^2 = 4k^2+4k+1 = 4k(k+1)+1$$ Why must this leave a remainder of $1$ when divided by $8$?

Answer 2

If $n$ is odd, then $n$ is of the form $2k+1$. Then $n^2 = 4k^2 + 4k+1 = 4k(k+1)+1$. Now, for any $k$, we see the first term is divisible by $8$ since $k(k+1)$ is even. The remainder must be $1$ then.

Answer 3

$$(2k + 1)^2 = 4 k^2 + 4 k + 1 = 4 (k+1) k + 1$$

Since either $k$ or $k+1$ is even, we get $4 (k+1)k$ is divisible by $8$, proving your claim.

Answer 4

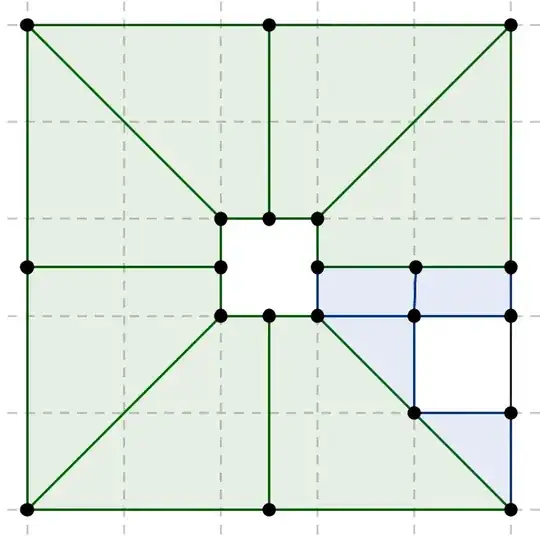
Consider a $n\times n$ grid minus the central square. You may divide such "square annulus" in eight parts with the same area, in such a way that each part has an even number of halved (horizontally, vertically or diagonally) squares, so the area of each part is an integer.

Answer 5

An odd number either one more or one less than a multiple of 4: i.e. $n=4m\pm1$. So $(4m\pm1)^2= 16m^2\pm8m+1$, as the first two terms are multiples of 8, an odd square is indeed 1 mod 8.