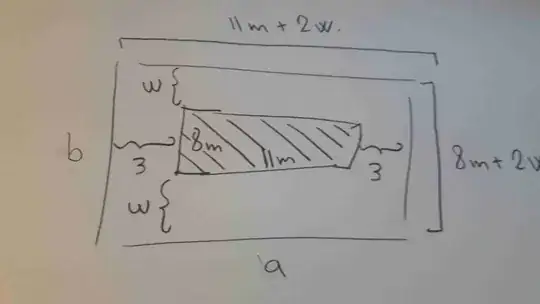
A rectangular swimming pool with dimensions of 11m and 8m is built in a rectangular backyard. The area of the backyard is 1120m^2. If the strip of yard surrounding the pool is of uniform width, how wide is the strip?
So I tried to find a diagram but it doesn't seem to make sense because the backyard could have any dimensions...so i made the backyard 28 by 40 and then the answer would be 8.5 and 16 which isn't correct.