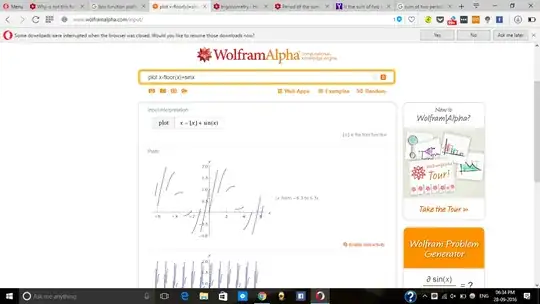
The function is:
$f(x)= x-[x]+sinx$ where [x] is the greatest integer function.
The time period of $x-[x]$ is $1$ and $sin x$ is $2\pi$
And the time period of $f(x)$ is the LCM of the above given time periods(source)
So here,
$LCM(1,2\pi)=2\pi$
Therefore $f(x)$ must have $2\pi$ as it's time period.But if I plot is graph $f(x)$ doesnot look like a periodic function.Why?
It isn't periodic because the least common multiple of $1$ and $2\pi$ doesn't exist (multiples here mean integer multiples). What can be done is to change $x$ in $\sin x$ to $\sin(2\pi x)$ (or really any integer multiple of $\pi$) or change $x-\lfloor x\rfloor$ to $\frac{x}{2\pi}-\lfloor\frac{x}{2\pi}\rfloor$.
The key is that after the change, the periods of both functions differ by a rational (hence a natural number) multiple... This guarantees the existence of a least common multiple.
For example, $f(0)=0$, but $f(2 \pi )=2 \pi -[2 \pi]+\sin(2\pi)=2\pi -[2\pi]\neq 0$.
$f(x)= x-[x]+sinx$ where [.] is the greatest integer function.
The period of $x-[x]=${$x$} is $1$ and $sin x$ is $2\pi$. Here {.} is fractional part function.
And the period of $f(x)$ is the LCM of $1$ and $2\pi$. As LCM of a rational and irrational is undefined, the given function is non-periodic. Note :-LCM of a rational and irrational is undefined.
