4

The angle addition formulas in “regular” trigonometry state that

$\sin(\alpha+\beta)=\sin\alpha\cos\beta + \cos\alpha\sin\beta$

and

$\cos(\alpha+\beta)=\cos\alpha\cos\beta - \sin\alpha\sin\beta$

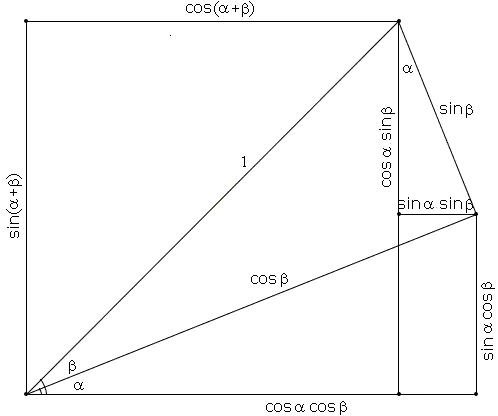
It is fairly straightforward and easy to derive these formulas from a figure like this:

angle addition proof

It is also easy to prove it using:

$\cos(x) = \frac{e^{ix} + e^{-ix}}2$

and

$\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$

Similar relations hold for the hyperbolic trig functions, namely

$\sinh(\alpha+\beta)=\sinh\alpha\cosh\beta + \cosh\alpha\sinh\beta$

$\cosh(\alpha+\beta)=\cosh\alpha\cosh\beta + \sinh\alpha\sinh\beta$

which again can be computed using

$\cosh(x) = \frac{e^{x} + e^{-x}}2$

$\sinh(x) = \frac{e^{x} - e^{-x}}2$

How would one prove the angle sum formulas for the hyperbolic functions from their geometric definition?

Community
  • 1
Remus Bleys
  • 69
  • Hope you don't mind my edit to your question. I think it makes it easier to have all the relevant information included in the post itself, so people don't have to follow links to images or look up the addition formulas. – MvG Sep 28 '16 at 06:43
  • I think the main problem here is that the argument of a hyperbolic function in the geometric definition is interpreted as an area, and it is very hard to visually see that two given areas are the same. So I doubt there will be an easy way to visualize this relationship. – MvG Sep 28 '16 at 06:46
  • Just as an FYI: My answer here derives the exponential formulas for $\sinh u$ and $\cosh u$ from the geometric definitions (using a pinch of Calculus). – Blue Sep 28 '16 at 19:12

0 Answers0