I am trying to devise a recursive prime-generating function following an intuition of a possible analogy to Mills and Wright prime-representing functions, in the present case based on logarithms. The proposed prime generating function $f(n)$ will provide not a subset but the complete set of primes being $f(1)=2$, $f(2)=3$, $f(3)=5$... and the prime-generating constant will be called $L$. As in the standard results from Mills and Wright the decimal precision of the constant is important in order to recover the embedded primes and it is not known if $\lim_{n \to \infty} L_n$ is rational or not.
This is how it works and the questions are at the end:
- Start with $n=1$, current prime $p_1=2$, previous accumulated value of the constant will be defined as $L_0=0$ (starting value). Calculate the value for the constant for $n=1$. It will be $$L_1=\frac{Ln(2+L_0)}{Ln(1+1)}$$
(Where $Ln$ is the natural logarithm).
- Calculate the value for the constant for $n=2$, $p_2=3$, $$L_2=\frac{Ln(3+L_1)}{Ln(2+1)}$$
So if we apply recursively the formula, for $n$:
$$L_n=\frac{Ln(p_n+L_{n-1})}{Ln(n+1)}$$
For instance, the following PARI_GP code calculates $L_{500}$
\p2000;
testlimit=500;current_pr=2;L=0;for(n=1,testlimit,L=log(current_pr+L)/log(n+1);current_pr=nextprime(current_pr+1););print("n is ",testlimit," and L is ",L);
$$L_{500} = 1.3159864456...$$
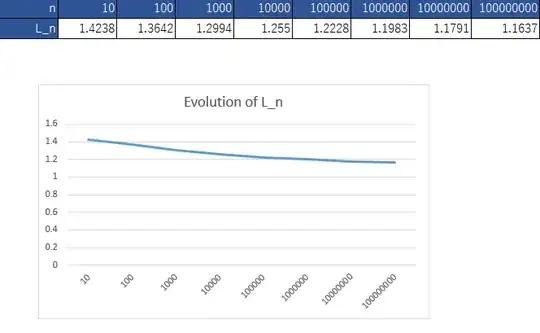
Reviewing the results of the tests, it seems that $\lim_{n \to \infty} L_n$ oscillates (due to the gaps between primes applied in the formula) but in the long term it is stable and tends to decrease and goes down to a value closer to $1$ and lower than $2$.
For example:
\p3;
testlimit=500000;current_pr=2;L=0;for(n=2,testlimit,L=log(current_pr+L)/log(n);current_pr=nextprime(current_pr+1););print("n is ",testlimit," and L is ",L);
$L_{5000}$ is around $1.23...$ and the above code shows that $L_{500000}$ is around $1.21$. Other similar tests show that it tends to go down to some specific limit near the lower bound of $[1,2]$.
As the proccess of recovering the primes is recursive, the way of using the constant is as follows:
For instance, assuming that we have $L_{500}$, we need to start obtaining the last prime back:
$$f(500)=p_{500}=\lfloor (500+1)^{L_{500}} \rfloor - 1 = 3571$$
Then recover $L_{499}$ and recover $f(499)=p_{499}$
$$L_{499}=((500+1)^{L_{500}})-p_{500}=1.31586811...$$
$$f(499)=p_{499}=\lfloor (499+1)^{L_{499}} \rfloor - 1 = 3559$$
$$...$$
So in general the recursive process to recover $L_{n}$ and $f(n)=p_n$ from $L_{n+1}$ and $f(n+1)=p_{n+1}$ is:
$$L_{n}=((n+2)^{L_{n+1}})-p_{n+1}$$
$$f(n)=p_{n}=\lfloor (n+1)^{L_{n}} \rfloor - 1$$
The following code, having $L_{500}$ calculates backwards the complete set of primes $\{p_{500}..p_{1}\}$
curr_L=L;for(n=1,testlimit,curr_n=testlimit-n+2;curr_p=(floor(curr_n^curr_L))-1;print("n is ",testlimit-n+1," ; Current prime is ",curr_p," and is_prime check = ",isprime(curr_p));curr_L=(curr_n^curr_L)-curr_p;);
There is a little correction required for the calculation of $p_1$. Depending on the $L_n$ calculated, sometimes the recovered value $\lfloor (2)^{L_{1}} \rfloor = 2$ instead of $3$. And for that reason, when the value is $2$, $f(1)=p_{1}=\lfloor (2)^{L_{1}} \rfloor - 1 = 2-1 = 1$ instead of the expected $p_1=2$. To handle this special case, we can express the prime-generating function as:
$$f(n)=p_{n}=\lfloor (n+1)^{L_{n}} \rfloor - 1 + \delta_{f(n),2}$$
Where $\delta_{f(n),2}$ is the Kronecker delta function (kindly provided by @MitchellSpector in this question). Basically it is a little trick that will assure that always $f(1)=2$ independently of the value of $\lfloor (n+1)^{L_{n}} \rfloor$ ($2$ or $3$). It would be possible a definitions-by-case of $f(n)$ as well instead of using one single expression.
This is a graph of the evolution of $L_n$ (only four decimals of precision):
I would like to ask the following questions:
Are the calculations correct or is there a mistake in the assumptions?
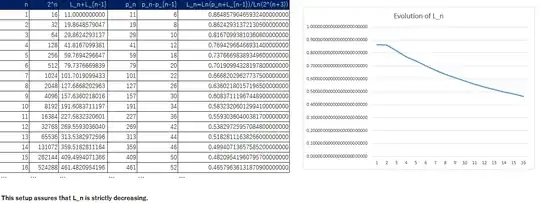
How could I prove that $L_n$ is decreasing in the long term and there is indeed a limit? The tests show that but I am a little bit lost about how to demonstrate that it really is decreasing (because each step depends on the gaps between primes). A hint about the starting step would be great!
Initially I think this kind of recursive prime-generating function is a little bit different from the original results of Mills and towers of powers of Wright, but it might be possible that a similar idea had been explored before in recent literature. Initially I did not find such references. Are there similar solutions as the one I am devising? Any references to papers would be very appreciated. Thank you!