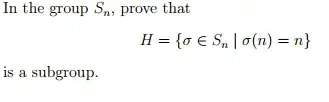Permutation group isomorphism

Question

I've already proved H is a subgroup as it was very straight forward and easy. I'm certain there is an extremely obvious and easy isomorphism that I am somehow missing. Thanks for any help.

score 2 · Accepted Answer · answered Sep 21 '16 at 20:08

2

Define $\phi:S_{n-1}\to S_n$ as follows: If $\sigma\in S_{n-1}$, let $\phi(\sigma)\in S_n$ be the map $\phi(\sigma)(k)=\sigma(k)$ for $k<n$ and $\phi(\sigma)(n)=n$.

answered Sep 21 '16 at 20:08

David Hill

12,165

Thanks, that makes sense to me. I haven't done algebra in a while so I'm still slowly processing the basics again. Thank you very much! – SenoritaChad Sep 21 '16 at 20:13

score 0 · Answer 2 · edited Apr 13 '17 at 12:19

0

The subgroup $H$ has index $n$ is $S_n$, so must be isomorphic to $S_{n-1}$, as we have seen here. But of course, it is much more straightforward to write down an isomorphism.

edited Apr 13 '17 at 12:19

Community

1

answered Sep 21 '16 at 20:13

Dietrich Burde

130,978

Yes I noticed that, which is why I thought the answer would be so obvious, I was just having a lot of troubles figuring out a specific isomorphism. Thanks! – SenoritaChad Sep 21 '16 at 20:15

score 0 · Answer 3 · answered Sep 21 '16 at 20:21

For any $\sigma\in H$, consider its restriction to the set $\bigl\{1,\dots, n-1\bigr\}$.

This restriction of $\sigma$ takes its values in $\bigl\{1,\dots, n-1\bigr\}$, by definition of $H$, so restricting its codomain to $\bigl\{1,\dots, n-1\bigr\}$ makes it a permutation of $S_{n-1}$.

Permutation group isomorphism

3 Answers3