I have the length of n sides $[l_1,l_2,...,l_n]$ and it is possible to form a polygon using these sides. The sides of the polygon will be in the order as given so the adjacent sides of $l_1$ are $l_n$ and $l_2$ and like that. How do I find the interior angles of the polygon? I know there can be multiple lists of angles for 1 list of sides, I just need any one.
Asked
Active
Viewed 976 times
4
-
Note that if one length $\ell_i $ exceeds the sum of the others, no polygon is possible. Do you care whether the polygon constructed is convex? – hardmath Sep 17 '16 at 12:29
-
Yes, the polygon should be convex and lengths are such that it is possible to form a convex polygon. No $L_i$ exceeds the sum of the others. – sam1064max Sep 17 '16 at 12:38
-
One approach that uniquely determines interior angles is to require the polygon of maximum area enclosed. See whether the answers to that recent Question are useful to you. – hardmath Sep 18 '16 at 02:39
1 Answers
3
Two suggestions:
(1) Use the "2-kinks" theorem to form a triangle from your lengths. (Computational Geometry in C, p.330). Then several angles are $180^\circ$, and three are triangle angles.
(2) Form a cyclic polygon from your lengths by shrinking the radius of a circle until your lengths close to a polygon:
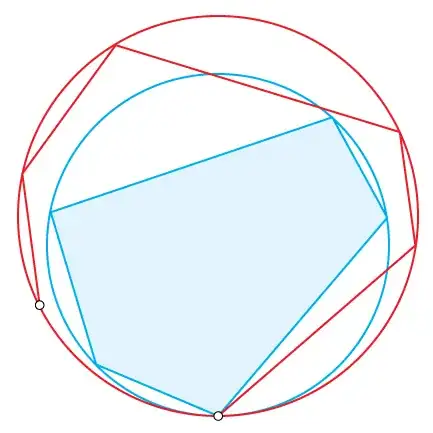
See this MSE posting for cyclic polygon calculations, or the reference by @hardmath (in a comment) to another MSE posting on cyclic polygons.
Joseph O'Rourke
- 30,327