Prove $\int_0^{\pi/2}{\frac{1+2\cos 2x\cdot\ln\tan x}{1+\tan^{2\sqrt{2}} x}}\tan^{1/\sqrt{2}} x~dx=0$

Question

I'm curious, how one can prove the following integral $$ \int_0^{\pi/2}{\frac{1+2\cos 2x\cdot\ln\tan x}{1+\tan^{2\sqrt{2}} x}}\tan^{1/\sqrt{2}} x~dx=0 $$ Here is the Wolfram Alpha computation which shows that it is correct to at least 45 digits.

My attempt: I knew the integral $$ \int_0^{\pi/2}\frac{1}{1+\tan^\alpha\phi}d\phi=\int_0^{\pi/4}\frac{1}{1+\tan^\alpha\phi}d\phi+\int_0^{\pi/4}\frac{\tan^\alpha\phi}{1+\tan^\alpha\phi}d\phi=\frac{\pi}{4} $$ which can be calculated for all values of $\alpha$. I tried to find an analogous symmetry that will allow me to cancel all the terms also in this case, but so far no luck. I also suspect that this integral might be related to derivative of Herglotz integral. Herglotz showed that $$ \int_{0}^{1} \frac{\ln\left(1 + t^{\,{\large\alpha}}\right)}{1 + t}\,{\rm d}t $$ can be computed for some algebraic values of $\alpha$, e.g. $\alpha=4+\sqrt{5}$. If we take derivative of this integral with respect to $\alpha$ then we get $$ \int_{0}^{1} \frac{t^\alpha\ln t}{(1 + t)(1+t^\alpha)}\,{\rm d}t $$ Change of variables $t=\tan^2\phi$ gives $$ 4\int_{0}^{\pi/4} \frac{\tan^{2\alpha+1}\phi\cdot\ln \tan\phi}{1+\tan^{2\alpha}\phi}\,{\rm d}\phi $$ which looks quite similar to the integral under consideration.

Answer 1

Disclaimer. This is not an answer! But I hope the following transformations and numerical experiments can be useful in finding the solution.

First, we will get rid of trigonometric functions. Setting $t=\tan \phi$ we obtain:

$$\int_0^\infty \frac{t^a [1+t^2+2(1-t^2) \ln t]}{(1+t^b)(1+t^2)^2}dt$$

Here $a=\frac{1}{2}\sqrt{2}$, $b=2\sqrt{2}$. It makes sense to pose a more general problem with $a=\frac{1}{2}c$, $b=2c$ for some real parameter $c$.

Thus we have:

$$I(c)=\int_0^\infty \frac{t^{c/2} [1+t^2+2(1-t^2) \ln t]}{(1+t^{2c})(1+t^2)^2}dt$$

Here is a plot of $I(c)$. There appear to be only two roots $c= \pm \sqrt{2}$ - the function appears to be even.

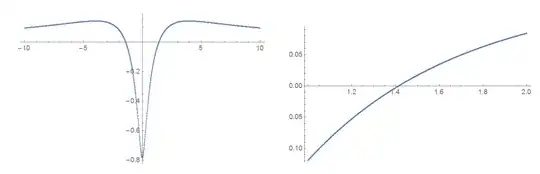
It's easy to prove that $I(c)=I(-c)$. Let's set $t=\frac{1}{u}$:

$$I(c)=-\int_\infty^0 \frac{u^{-c/2} [1+u^{-2}-2(1-u^{-2}) \ln u]}{u^2(1+u^{-2c})(1+u^{-2})^2}du$$

Multiplying both sides by $u^2$ we obtain:

$$I(c)=\int_0^\infty \frac{u^{-c/2} [1+u^2+2(1-u^2) \ln u]}{(1+u^{-2c})(1+u^2)^2}du=I(-c)$$

---

Let's separate the integral into to parts: $$I=\int_0^\infty=\int_0^1+\int_1^\infty$$

Making the substitution $t=\frac{1}{u}$ we obtain:

$$\int_1^\infty \frac{t^{c/2} [1+t^2+2(1-t^2) \ln t]}{(1+t^{2c})(1+t^2)^2}dt=\int_0^1 \frac{u^{3c/2} [1+u^2+2(1-u^2) \ln u]}{(1+u^{2c})(1+u^2)^2}du$$

Thus, we can introduce another form of the integral with finite limits:

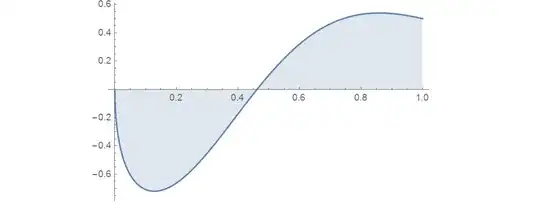
$$I(c)=\int_0^1 \frac{t^{c/2}(1+t^c) [1+t^2+2(1-t^2) \ln t]}{(1+t^{2c})(1+t^2)^2}dt$$

The plot of the integrand is presented below:

Because now $0<t<1$ we can expand a part of the integrand into a series:

$$I(c)=\sum_{k=0}^\infty (-1)^k \int_0^1 \frac{t^{(2k+1/2)c}(1+t^c) [1+t^2+2(1-t^2) \ln t]}{(1+t^2)^2}dt$$

Expanding the numerator we obtain $8$ integrals in the form:

$$\int_0^1 \frac{t^\alpha}{(1+t^2)^2} dt \quad \text{and} \quad \int_0^1 \frac{t^\alpha \ln t}{(1+t^2)^2} dt$$

The first integral can be evaluated using the digamma function while the second integral can be obtained by differentiating the first w.r.t. $\alpha$.

Thus, the integral is equal to the following series:

$$I(c)=\frac{1}{16} \sum_{k=0}^\infty (-1)^k \times$$

$$ \times \left[ 4 \left(\psi\left(\frac{c (4 k+1)+2}{8}\right)-\psi \left(\frac{c (4 k+1)+2}{8}+\frac{1}{2}\right)\right)+ \\ +4 \left(\psi \left(\frac{c (4 k+3)+2}{8}\right)-\psi \left(\frac{c (4 k+3)+2}{8}+\frac{1}{2}\right)\right)+ \\ +c (4 k+1) \left(\psi ^{(1)}\left(\frac{c (4 k+1)+2}{8}\right)-\psi ^{(1)}\left(\frac{c (4 k+1)+2}{8}+\frac{1}{2}\right)\right)+ \\ +c (4 k+3) \left(\psi ^{(1)}\left(\frac{c (4 k+3)+2}{8}\right)-\psi ^{(1)}\left(\frac{c (4 k+3)+2}{8}+\frac{1}{2}\right)\right) \right]$$

This seems too complicated, but I have hope that some properties of the digamma function can help in showing that $I(\sqrt{2})=0$.

---

A little more generalization. Consider the integral with two parameters:

$$I(a,b)=\int_0^\infty \frac{t^a [1+t^2+2(1-t^2) \ln t]}{(1+t^b)(1+t^2)^2}dt=$$

$$=\int_0^1 \frac{(t^a+t^{b-a}) [1+t^2+2(1-t^2) \ln t]}{(1+t^b)(1+t^2)^2}dt$$

$$I(a,b)=I(b-a,b)$$

The curve $I(a,b)=0$ is represented below:

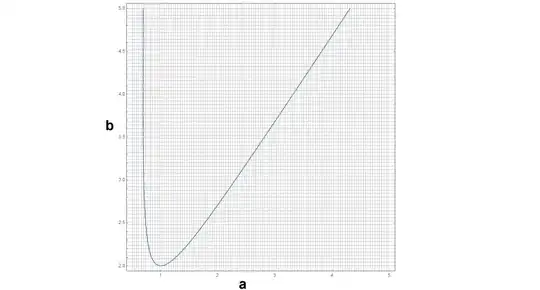
We see it has two branches. So far I haven't been able to find other algebraic pairs on it except for:

$$I \left(\frac{1}{2} \sqrt{2},2\sqrt{2} \right)=0 \\ I \left(\frac{3}{2} \sqrt{2},2\sqrt{2} \right)=0$$

And the trivial one:

$$I(1,2)=0$$

---

Update:

The integral can be simplified in the following way:

$$\int_0^\infty \frac{t^a [1+t^2+2(1-t^2) \ln t]}{(1+t^b)(1+t^2)^2}dt=\frac{1}{2} \int_0^\infty \frac{t^{a-1} [1+t^2+2(1-t^2) \ln t]}{(1+t^b)(1+t^2)^2}dt^2$$

Introducing $v=t^2$, $\alpha=\frac{a-1}{2}$ and $\beta=\frac{b}{2}$ we need to investigate:

$$J(\alpha,\beta)=\int_0^\infty \frac{v^{\alpha} [1+v+(1-v) \ln v]}{(1+v^\beta)(1+v)^2}dv=\int_0^1 \frac{(v^{\alpha}+v^{\beta-\alpha-1}) [1+v+(1-v) \ln v]}{(1+v^\beta)(1+v)^2}dv$$

$$J(\alpha,\beta)=J(\beta-\alpha-1,\beta)$$

This integral seems much better. We now need to prove that:

$$J\left(\frac{\sqrt{2}-2}{4},\sqrt{2} \right)=0$$ or $$J\left(\frac{3\sqrt{2}-2}{4},\sqrt{2} \right)=0$$

---

Update 2:

Some further work on the integral. From the comment of @user90369 we introduce a new form of the integral:

$$Y(A):=\int_0^\infty \frac{\cosh Ax}{\cosh 2Ax} \frac{\cosh x-2x \sinh x}{\cosh^2 x} dx$$

Setting $t=e^x$ we obtain:

$$Y(A)=2 I(2A)$$

Separating the integral into two parts and introducing a new parameter $P$ we have:

$$Y_1(A,P):=\int_0^\infty \frac{\cosh Ax}{\cosh 2Ax} \frac{1}{\cosh P x} dx$$

$$Y_2(A,P):=-2\int_0^\infty \frac{\cosh Ax}{\cosh 2Ax} \frac{x \sinh P x}{\cosh^2 P x} dx=2\frac{\partial}{\partial P} Y_1(A,P)$$

Thus, we can work with $Y_1$ first:

$$Y_1(A,P)=\frac{1}{A} \int_0^\infty \frac{\cosh y}{\cosh 2y} \frac{1}{\cosh p y} dy$$

Here $p=P/A$. Setting $e^y=z$ we obtain:

$$Y_1(p):=\int_0^\infty \frac{\cosh y}{\cosh 2y} \frac{1}{\cosh p y} dy=2 \int_0^1 \frac{1+z^2}{1+z^4} \frac{z^p}{1+z^{2p}} dz=\int_0^\infty \frac{1+z^2}{1+z^4} \frac{z^p}{1+z^{2p}} dz$$

Despite @Lucian's comment, I can't represent $Y_1(p)$ in terms of Beta function in closed from, only as a series, but it might be possible. I would wager a closed form in terms of hypergeometric functions.

For particular values of $p$ there are closed forms. So far I've found closed forms for $p=(0,1/4,1/3,1/2,2/3,1,2,3,4,5)$. They are all algebraic multiples of $\pi$. But to evaluate the original integral, we need the closed form for general $p$. Seethis question.

---

Update 3:

If we allow double sums we can express the problem in a compact and almost symmetrical way:

Prove that for $B=\sqrt{2}$: $$\sum_{k,n=0}^\infty (-1)^{k+n} \frac{4k+1-(2n+1)B}{(4k+1+(2n+1)B)^2}=-\sum_{k,n=0}^\infty (-1)^{k+n} \frac{4k+3-(2n+1)B}{(4k+3+(2n+1)B)^2}$$

Answer 2

This answer builds on observations made by user90369 and Yuriy S. They define the functions $$ Y_1(A,P):=\int_0^\infty \frac{\cosh Ax}{\cosh 2Ax} \frac{1}{\cosh P x} dx,\tag{1} $$ $$ Y_2(A,P):=-2\int_0^\infty \frac{\cosh Ax}{\cosh 2Ax} \frac{x \sinh P x}{\cosh^2 P x} dx=2\frac{\partial}{\partial P} Y_1(A,P),\tag{2} $$ and then note that OPs conjecture is equivalent to $Y_1(1/\sqrt2,1)+Y_2(1/\sqrt2,1)=0$.

I happened to notice that $(1)$ is an integral of a product of two self-reciprocal functions $\sqrt{\frac{2}{\pi}}\int_0^\infty f(x)\cos ax dx=f(a)$ (functions 3 and 4 in this list): $$ f_1(x)=\frac{1}{\cosh\sqrt{\frac{\pi}{2}}x},\quad f_2(x)=\frac{\cosh \frac{\sqrt{\pi}x}{2}}{\cosh \sqrt{\pi}x}.\tag{3} $$

For any such two functions Ramanujan shows that (simple proof is outlined in this answer) $$ \int_0^\infty f_1(x)f_2(\alpha x) dx= \frac{1}{\alpha}\int_0^\infty f_1(x)f_2(x/\alpha) dx.\tag{4} $$

Substituting $(3)$ in $(4)$ one obtains $$ \int_0^\infty \frac{1}{\cosh\sqrt{\frac{\pi}{2}}\alpha x}\frac{\cosh \frac{\sqrt{\pi}x}{2}}{\cosh \sqrt{\pi}x} dx= \frac{1}{\alpha}\int_0^\infty \frac{1}{\cosh\sqrt{\frac{\pi}{2}}x/\alpha}\frac{\cosh \frac{\sqrt{\pi}x}{2}}{\cosh \sqrt{\pi}x} dx, $$ and after trivial algebra $$ \int_0^\infty \frac{1}{\cosh\alpha x}\frac{\cosh \frac{x}{\sqrt{2}}}{\cosh \sqrt{2}x} dx= \frac{1}{\alpha}\int_0^\infty \frac{1}{\cosh x/\alpha}\frac{\cosh \frac{x}{\sqrt{2}}}{\cosh \sqrt{2}x} dx. $$ This gives the functional equation $$Y_1(1/\sqrt{2},P)=\frac{1}{P}Y_1(1/\sqrt{2},1/P).$$ Differentiating this functional equation with respect to $P$ one obtains $$ \frac12 Y_2(1/\sqrt{2},P)=-\frac{1}{P^2}Y_1(1/\sqrt{2},1/P)-\frac{1}{2P^3}Y_2(1/\sqrt{2},1/P), $$ which gives at $P=1$ the required relation $$ Y_1(1/\sqrt2,1)+Y_2(1/\sqrt2,1)=0. $$

Answer 3

This is not a complete answer, but I think this is a possible solution. If you apply the change of variable $t=\tan(x)$, the original integral can be writen as

$$\int_{0}^{\infty}\frac{1 + 2\left(\frac{1-t^{2}}{1+t^{2}}\right)\log(t)}{1+t^{2\sqrt{2}}}t^{1/\sqrt{2}}\frac{dt}{t^{2} + 1} = \int_{0}^{\infty}\frac{t^{1/\sqrt{2}}}{(t^{2} + 1)(1+t^{2\sqrt{2}})}dt + \int_{0}^{\infty}\frac{2(1-t^{2})\log(t)}{(t^{2} + 1)^{2}(1+t^{2\sqrt{2}})}t^{1/\sqrt{2}}dt,$$

and this integral would be solved by the method of residues for Mellin Transformations.

Checks Pags. 60-62 of http://jacobi.fis.ucm.es/artemio/Notas%20de%20curso/VC.pdf (I couldn't find an english version)