In a course I had, we have been given two statements P and Q and their "boolean table" :
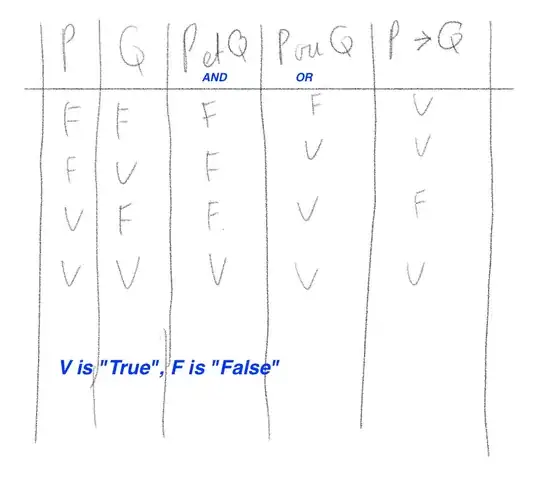
While I completely understand P and Q and P or Q values, I can't understand the first two lines for P->Q, why is the result true even when P is false ?
Thank you.