0

The number of four digit numbers that are less than 2003 and the sum of whose digits is less than the sum of the digits of 2003 is ?

Here we are looking for four digit numbers whose sum of digits is 1,2,3 or 4.

2000,2001 and 2002 are the only numbers greater than 2000 that will be part of our set.

Now I know, first digit of the rest of the numbers can only be 1. How to proceed from here ?

Here is the solution,

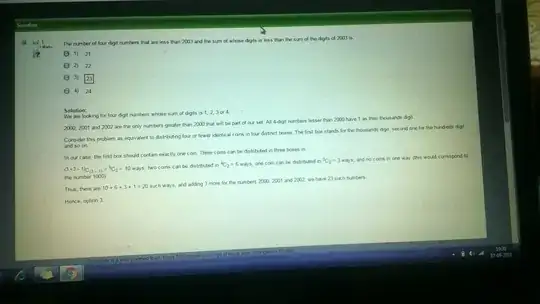
solution

but I don't understand how this problem can be considered as equivalent to distributing four or fewer identical coins in four distinct boxes.

Any help would be appreciated.

mac07
  • 165
  • 1
    Just think of a #coins in box as a number. Hence you are left with 4 coins/sum of digits to distribute. You can either put them in place 2,3,4 or dont distribute all digits (fourth box). Hence putting 2 coins in first box, none in second, 1 in third, 1 in fourth you will get the number 1-2-0-1=1201 (+1 coin ignored, since 1+2+0+1=4=5-1). TL,DR; #boxes = number of places digits can be put +1 (ignore box), #coins = sum of digits to be distributed – ctst Sep 09 '16 at 14:57

1 Answers1

1

The statement "this problem can be considered as equivalent to distributing four or fewer identical coins in four distinct boxes" is incorrect.

Since we are talking of numbers, the first digit can't be $0$, and the correct statement of the problem should be that apart from the numbers $2000,2001,2002,\;$this problem can be considered as equivalent to distributing three or fewer identical coins in three distinct boxes

Then, applying stars and bars, we get $\binom52 + \binom42 + \binom32 +\binom22 +3 = 23$

true blue anil
  • 41,295
  • @anil Okay , apart from the numbers 2000,2001,2002 this problem can be considered as equivalent to distributing three or fewer identical coins in three distinct boxes because more than 3 makes the sum greater than or equal to 5 right? – mac07 Sep 09 '16 at 17:50
  • Yeah, that's right. (Bear in mind, the first digit is already $1$ to start with) – true blue anil Sep 09 '16 at 19:16
  • @Anil Can you suggest a good source of combinatorics tutorial for a beginner like me? – mac07 Sep 10 '16 at 06:17
  • 1
    You could look at suggestions in http://math.stackexchange.com/questions/1867907/material-to-learn-some-basic-combinatorics/1887488#1887488 as well as related questions on MSE. – true blue anil Sep 10 '16 at 07:28