2

I have to solve this problem:

Compute the value of the integral $$\int _0 ^\infty \frac{x^\alpha}{1+x^2}\, \mathrm d x,\quad -1<\alpha<1$$

Which is in my Complex Analysis textbook, so I assume I have to solve it using Complex Analysis even if the integral is real.

I tried integrating by parts: $$\int _0 ^\infty \frac{x^\alpha}{1+x^2}\, \mathrm d x=\left.\vphantom {\frac{1}{2}}x^\alpha \arctan x \right\vert_0 ^\infty - \int _0 ^\infty \alpha x^{\alpha-1}\arctan x\, \mathrm d x$$ But this does not make sense, as the limit depends on the sign of $\alpha$. And surely there is another way that I am missing. Also, I don't know how to use the fact that $\alpha \in (-1,1)$.

Did
  • 279,727
Miguel Mars
  • 1,017
  • If you want it to solve it using complex analysis, you need to choose the right contour integral (https://en.wikipedia.org/wiki/Methods_of_contour_integration), considering that the poles lie at $x=\pm i$ and the correct branch to deal with the $x^\alpha$. Besides: that $\alpha<1$ is very helpful, as this allows you to do $ML$ estimates when you are taking radii going to infinity. – b00n heT Sep 08 '16 at 12:00

2 Answers2

3

By substituting $x=\tan\theta$ and exploiting Euler's beta function and the reflection formula for the $\Gamma$ function we have $$ I(\alpha)=\int_{0}^{+\infty}\frac{x^\alpha}{1+x^2}\,dx = \color{red}{\frac{\pi}{2 \cos\left(\frac{\pi\alpha}{2}\right)}}$$ for any $\alpha\in(-1,1)$.

Jack D'Aurizio
  • 353,855
3

This is the same as @JackD'Aurizio's solution, with the steps filled in to make it a little easier to follow.

Let $z=x^2$ \begin{align} \int\limits_{0}^{\infty} \frac{x^{a}}{1+x^{2}} \mathrm{d}x &= \frac{1}{2} \int\limits_{0}^{\infty} z^{(a-1)/2} \frac{\mathrm{d}z}{1+z} \\ \tag{a} &= \frac{1}{2} \mathrm{B}\left(\frac{a+1}{2}, 1-\frac{a+1}{2} \right) \\ \tag{b} & = \frac{1}{2} \Gamma\left(\frac{a+1}{2}\right) \Gamma\left(1-\frac{a+1}{2}\right) \\ \tag{c} &= \frac{\pi}{2\sin(\pi(a+1)/2)} \end{align} a. We used the following definition of the beta function $$\mathrm{B}(a.b)=\int\limits_{0}^{\infty} \frac{z^{a-1}}{1+z^{a+b}} \mathrm{d}z$$ b. $$\mathrm{B}(a.b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$$ c. Euler reflection formula. $$\Gamma(1-z)\Gamma(z)=\frac{\pi}{\sin(\pi z)}$$

We can also evaluate this integral via contour integration. Let \begin{equation} f(z) = \frac{z^{a}}{1+z^{2}} \end{equation} Using the keyhole contour, we have first order poles at $\pm i$, so the residues are \begin{equation} \mathrm{Res}[f(z),i] = \frac{i^{a}}{i2} = \mathrm{e}^{ia\pi/2} \frac{1}{i2} \end{equation} \begin{equation} \mathrm{Res}[f(z),-i] = \frac{(-i)^{a}}{-i2} = -\mathrm{e}^{ia\pi} \mathrm{e}^{ia\pi/2} \frac{1}{i2} \end{equation}

\begin{align} \oint\limits_{C} f(z) \mathrm{d}z &= \pi \mathrm{e}^{ia\pi/2} \left(1 - \mathrm{e}^{ia\pi} \right) \\ &= \lim_{\epsilon,R \to 0,\infty} \int\limits_{\epsilon}^{R} f(x) \mathrm{d}x + \int\limits_{\Gamma} f(z)\mathrm{d}z + \int\limits_{R}^{\epsilon} f(x) \mathrm{d}x + \int\limits_{\gamma} f(z)\mathrm{d}z \\ &= \int\limits_{0}^{\infty} \frac{x^{a}}{1+x^{2}} \mathrm{d}x \,- \int\limits_{0}^{\infty} \mathrm{e}^{ia2\pi} \frac{x^{a}}{1+x^{2}} \mathrm{d}x \\ &= \left(1 - \mathrm{e}^{ia2\pi} \right) \int\limits_{0}^{\infty} \frac{x^{a}}{1+x^{2}} \mathrm{d}x \end{align}

Thus we have \begin{align} \int\limits_{0}^{\infty} \frac{x^{a}}{1+x^{2}} \mathrm{d}x &= \pi \mathrm{e}^{ia\pi/2} \left(1 - \mathrm{e}^{ia\pi} \right) \frac{1}{\left(1 - \mathrm{e}^{ia2\pi} \right)} \\ &= \frac{\pi \sin(a\pi/2)}{\sin(a\pi)} \\ &= \frac{\pi}{2\cos(a\pi/2)} \end{align}

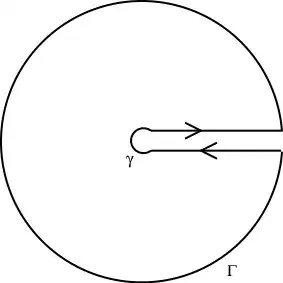
enter image description here

Notes:

  1. R is the radius of the large circle $\Gamma$.

  2. $\epsilon$ is the radius of the small circle $\gamma$.

poweierstrass
  • 2,388