4

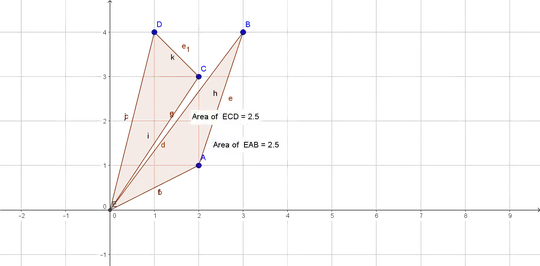
I am trying to understand why, geometrically, we have that

$$ \det(A) = \det(A^T). $$

To build intuition, I am thinking in 3 dimensions. So let $A$ be a $3 \times 3$ matrix of real numbers.

First, I know that if

$$ \det(A) = \left| \begin{array} xx_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{array} \right| $$

then $|\det(A)|$ can be thought of as the area of a parallelepiped formed by $(x_1, x_2, x_3)$, $(y_1, y_2, y_3)$, and $(z_1, z_2, z_3)$.

Moreover, the fact that $\det(A) = \det(A^T)$ implies that $|\det(A)|$ can also be thought of as the area of the parallelepiped formed by

$(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, and $(x_3, y_3, z_3)$.

Question: Does this also mean that the area of a parallelepiped formed by any permutation of the $x_i$, $y_i$, and $z_i$ is equal to $|\det(A)|$? For example, does the area of a parallelepiped formed by the coordinates $(x_1, y_2, z_3)$, $(x_2, y_1, z_2)$, and $(x_3, y_3, z_1)$ equal $|\det(A)$|?

Martin Sleziak
  • 53,687
user1770201
  • 5,195
  • 6
  • 39
  • 71
  • 1
    Possible duplicate of Determinant of transpose? – Alex Ortiz Sep 06 '16 at 18:00
  • @AOrtiz, the title of the question certainly suggests it is a duplicate of the question you linked to. However, the question at the end of the post seems quite different from what the title suggests. I don't think this is a duplicate (of that question at least). A bit of a misleading title... – TravisJ Sep 06 '16 at 18:32

2 Answers2

3

enter image description here

Here is a 2D example.

$$\begin{pmatrix} 2&3\\ 1&4\\ \end{pmatrix} \mapsto_{transpose} \begin{pmatrix} 2&1\\ 3&4\\ \end{pmatrix}$$

I'm still thinking of a satisfying (geometric) explanation as to why this always works, but pictures are always good.

Dan L
  • 653
  • I really like this picture. As for the geometric explanation, for the 2d case I think you might be able to use Heron's formula: https://en.wikipedia.org/wiki/Heron%27s_formula, specifically the version $A= \frac{1}{4} \sqrt{4 a^2b^2 - (a^2 + b^2 -c^2)^2}$. If we have a matrix $$M = \begin{bmatrix} m_1 & m_2 \ m_3 & m_4 \end{bmatrix}$$ then $a^2 = m_1^2 + m_3^2, b^2 = m_2^2 + m_3^2, c^2 = (m_2 - m_1)^2 + (m_4 - m_3^2)$. When we take the transpose $M^T=M'$, then in the formula for $A'$, we have $a^2= m_1^2 + m_2^2, b^2 = m_3^2 + m_4^2, c^2 = (m_4-m_2)^2+(m_3-m_1)^2$. – Chill2Macht Sep 06 '16 at 23:49
  • Clearly for both triangles $a^2 + b^2$ is the same, although $c^2$ is not. However, the term $4a^2b^2=(2ab)^2$ compensates exactly for the difference. – Chill2Macht Sep 06 '16 at 23:51
1

Short answer is no.

For example suppose that $A$ is the identity matrix. The vectors are then $(x_1, y_1, z_1)=(1,0,0)$, $(x_2, y_2, z_2)=(0,1,0)$, and $(x_3,y_3,z_3)=(0,0,1)$. And $\text{det}(A)=1$. However, you could make a permutation $(x_1, y_2, z_3)=(1, 1, 1)$ and $(x_2, y_1, z_1)=(0, 0, 0)$ and $(x_3, y_3, z_2)=(0, 0, 0)$. The volume enclosed by those vectors is certainly not 1--in fact it is $0$.

TravisJ
  • 7,426
  • 1
    It is preserved, however, if you permute rows or columns. You just can't permute in a way that can't be done by permuting rows and columns. To be clear, the area remains the same, though the sign of the determinant can change. – abnry Sep 06 '16 at 18:07
  • @abnry, I think you meant to comment on the question (not this answer). The example provided by the OP includes permutations other than just permuting the rows. – TravisJ Sep 06 '16 at 18:09