Conditional statements?

Question

My textbook states that for the conditional statement "p implies q",

"p is a sufficient condition for q and q is a necessary condition for p."

How is this so? One might be lead to believe that p is independent of q and that it is a necessary and sufficient condition for q, no?

Additionally, what is the correct way to interpret the truth table of this conditional statement given below:

Edit: Please keep in mind that I have only just graduated high school and am not taking any advanced courses in logic.

Answer 1

It's important to realize that $p \implies q$ is not any kind of causative relationship - it's not saying $p$ causes $q$, or anything like that. It's saying "if $p$ happens to be true, then $q$ also happens to be true, possibly by pure coincidence".

Likewise, "necessary condition" and "sufficient condition" don't say anything about causation. $q$ is a necessary condition for $p$ exactly if $p$ can only be true if $q$ is; $p$ is a sufficient condition for $q$ exactly if whenever $p$ is true, so is $q$ - possibly coincidentally.

So suppose we know that the sentence $p \implies q$ is true. Then we know that if $p$ happens to be true, so does $q$; that's what the $\implies$ symbol means. So $p$ can't be true if $q$ isn't - if it were the case that $p$ is true with $q$ false, our sentence $p \implies q$ would be false. But that's the definition of $q$ being a necessary condition for $p$! Likewise, $q$ has to be true whenever $p$ is, which means $p$ is a sufficient condition for $q$.

Notice that it doesn't work the other way around - $p \implies q$ doesn't mean $p$ is a necessary condition for $q$, because $q$ might be implied by other, unrelated things as well.

We remind that if $p \implies q$, then: - $q \implies - p$

Answer 2

These are other equivalent ways to say $p \implies q$ in English. Personally I think "$p$ implies $q$" is the clearest, but I suppose it is important to understand the other phrases, since people use them often. Here is the intended interpretation.

"$p$ is a sufficient condition for $q$": if you want to know if $q$ is true, then it is enough (sufficient) to know that $p$ is true. However, there may be other ways for $q$ to be true, so in this case you cannot say $p$ is a necessary condition for $q$. [As an example, if $p$ is "my favorite number is divisible by $4$" and if $q$ is "my favorite number is even," then knowing $p$ is true is enough (sufficient) to conclude that $q$ is true, but there are other ways for $q$ to be true without $p$ being true, e.g. the case where my favorite number is $2$.]

"$q$ is a necessary condition for $p$": simply, if $p$ is true, then $q$ must (necessarily) also be true. It is necessary in the sense that if $q$ were not true, then it would be impossible for $p$ to be true.

Answer 3

Sufficient: It is enough for $p$ to be true in order to conclude that $q$ is also true.

Necessary: If $q$ is not true, then $p$ has to be false. For if $p$ were true, it would imply that $q$ is also true, a contradiction.

Regarding your second question, the idea is that, when the antecedent is false, the conditional is "vacuously" true. For instance, the pythagorean theorem says that if a triangle has a right angle, then the square of the hypothenuse equals the sum of the squares of the other two sides. If we're not dealing with a right triangle, then its meaningless to apply this theorem, so we cannot claim it is false. To give an extreme example, the sentence:

"If D is a duck, then the square of its hypothenuse equals the sum of the squares of the other two sides."

Seems rather irrelevant to the validity of this theorem, and claiming it is false because that sentence is not true, isn't too reasonable.

Answer 4

If you think of $p \implies q$ being equivalent to the statement $\lnot p \lor q$ (verify this with your truth table), that might help clarify what that wordy statement is trying to say.

It is essentially saying that there are two ways in which the statement $p \implies q$ is true. Either when $p$ is not true or when $p$ is true and $q$ is true.

p is a sufficient condition for q: This means that if $P$ is true, $Q$ is guaranteed to be true. In other words, it is sufficient for $P$ to be true to guarantee that $Q$ is true.

q is a necessary condition for p: Essentially means $P$ can't be true without $Q$ being true. It is necessary that $Q$ is true for $P$ to be true but not sufficient because there can be a case where $Q$ is true but $P$ is false. In other words, if $Q$ is false, then $P$ must be false. but if $Q$ is true, you cannot guarantee that $P$ is true (this follows from the contrapositive: $\lnot P \implies \lnot Q$).

Edit: Why is the statement true if the antecedent is false?

When you make a logical statement such as $P \implies Q$, you are saying this entire statement is something that is always true. Thus under any circumstance, the statement must be true. This is where a lot of people get confused so an example would clarify.

If I make the statement for all $x$, $ \text{"if x is a puppy"} \implies \text{"x is cute"}$, then I am saying this statement is a correct statement in that it must always be true. Now let us consider different cases:

1. x is a puppy - Well we claim if x is a puppy, it must be cute and in this case x is a puppy so it is necessary that it is cute. If x is a puppy and it isn't cute, then we have messed up because the logical statement we made must always be valid! This is important to realize; there is no such situation where the logical claim you made should should be false and in this case, the claim you made is that if x is a puppy, it must be cute.
2. x is not a puppy - Now even in this case, our logical statement must stand. This is the case you are interested in because you asked, why is the statement true if the antecedent is false. Like I said, the statement must always be true and so whoever made $P \implies Q$, defined it so that it will be true in the case that P is not true. Think of it this way; if x is not a puppy, then we can make no conclusions about whether or not x is cute. x could be a vulture in which case it is not cute, or x could be a cat in which case it is cute. Either way, our logical statement needs to be valid and thus it is just defined as being true when x is not a puppy. It is not so much that the statement is true when the antecedent is false as it is that the statement is defined to be true when the antecedent is false.

In summary, when you make the statement $P \implies Q$, you are saying this statement is universally true. The claim that the statement is making is that whenever $P$ is true, you can safely conclude $Q$ is true and whenever $P$ is not true, you can't say anything about $Q$, and this is an airtight statement that is never going to be invalid or false for any case. So if somebody tries to disprove you by saying "hey, I found a case where P is false but Q is true, your statement is wrong", you can simply say that your statement makes no claims that if $P$ is false then $Q$ must be as well and thus even in this case, is a valid statement.

Answer 5

Edit: I recently came across a neat illustration for how conditional statements behave. It was presented by Mark Zegarelli in Logic for Dummies:

(...) a slippery slide: Just step onto the if at the top of the slide and you end up sliding down into the then at the bottom.

A Truth Teller or a Liar

Dr. Joshua K. Lambert gives a good example:

We often refer to P in the compound statement "If P, then Q" as the hypothesis, while Q is commonly called the conclusion.

Upon first glance, the truth values associated with the implication seem to be a bit absurd when looking at the situations where P is false. We shall explain this using the following two statements.

P: You mow the lawn.

Q: You are paid $100.

We shall look at the implication of these two statements from a slightly different perspective. Instead of determining truth values let us look at this in the context of being a truth teller or a liar. Suppose a neighbor stated "If you mow the lawn, then you are paid $100." Notice that the previous sentence is just "P implies Q", and we will look at the different cases of truth values to see whether the neighbor was lying to you or telling the truth.

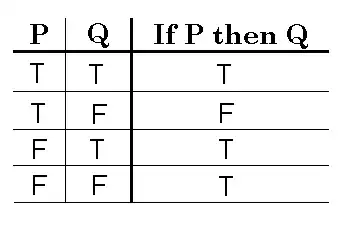
Case 1: We shall assume that P and Q are both true. This means that you did mow the lawn, and you were paid $100. Notice the neighbor told you the truth, which means the truth value for "P implies Q" would be true in this case.

Case 2: We shall assume that P is true and Q is false. This means that you did mow the lawn, but you never received $100. Notice the neighbor told you a lie in this case, which means the truth value for "P implies Q" would be false.

Case 3: We shall assume that P is false and Q is true. This means that you did not mow the lawn, and you were [paid] $100. Notice the neighbor never gave you any indication of what would happen if you did not mow the lawn. As a result, the neighbor was still telling the truth, which means the truth value for "P implies Q" would be true.

Case 4: We shall assume that P is false and Q is false. This means that you did not mow the lawn, and you never received $100. Notice the neighbor never gave you any indication of what would happen if you did not mow the lawn. As a result, the neighbor was still telling the truth, which means the truth value for "P implies Q" would be true.

Is p independent of q? Is p a necessary condition for q?

What is being evaluated is the value of the implication, if it holds as it is structured (if...then..., or P implies Q), as it was presented. In the given example, the neighbor lies only in Case 2, where p is true and q is false. In this case, the statement doesn't hold. We would have a basis to call him a liar or to say that his statement proved to be false concretely.

Cases 3 and 4 show us an important detail: "the neighbor never gave you any indication of what would happen if you did not mow the lawn." This is important because the statement is structured in the hypothesis of you mowing the lawn. The statement ("If you mow the lawn, you are paid \$100") is still true, even if the neighbor next door is handing out $100 bills or if you just decide that it's ok to stay at home and chill. The statement still holds itself under its hypothesis.

So p is not independent of q, because the structure ties them together, the hypothesis being false is not part of how the statement is composed. Even if we find another neighbor that states "If you do not mow the lawn, you are paid $100" (~p -> q), the case where p -> q would still be true as it was stated.

And p is not a necessary condition for q. If p is true, then it surpassed the category of a hypothesis, and the conclusion must follow from it, otherwise, our neighbor would be lying, his statement wouldn't have held itself, because q is necessary for the "sake" of what he says. And if it was false (if you don't mow the lawn), the statement would still be valid, because the hypothesis is still open, the statement holds itself, because we simply did nothing about the lawn.