Probability of a piece of stick being a certain size?

Question

Suppose Alex has a one meter long wooden stick that Alex breaks randomly in two places such that the location of the breaks are independently distributed uniformly along the length of the wooden stick.

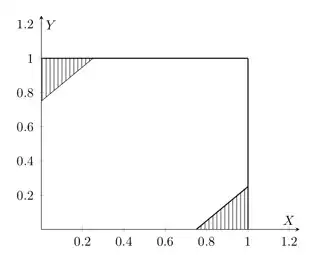
(a) Calculate the probability that one of the pieces will be more than 75 cm.

---

Is this just $\frac{75}{100}$?

---

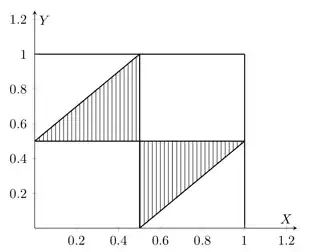
(b) Calculate the probability that the three resulting pieces of the stick can be arranged to form a triangle.

---

I know the stick cannot form a triangle unless all three pieces are no longer than the sum. But I don't know how to make this into a probability? If $\alpha$ is the first break and $\beta$ is the second break and L is the length of the stick, then $\alpha < \frac{L}{2}$ and $\beta < \frac{L}{2}$. How would I turn this into a probability?

Answer 1

Let the first point be located at a distance of $X$ and the second point be located at a distance of $Y$ from the start of the stick. We know that $X \sim U(0,1)$ and $Y \sim U(0,1)$.

Part (a)

For one of the line segments to be more than $0.75$ cm, then the following are the conditions where this is satisfied

$$ X > 0.75 \text{ and } Y > 0.75 \Rightarrow P(X > 0.75, Y > 0.75)=1/16 \\ Y < 0.25 \text{ and } X < 0.25, \Rightarrow P(Y < 0.25, X < 0.25)=1/16 \\ Y - X > 0.75 \text{ if } Y > X\\ X - Y > 0.75 \text{ if } X > Y $$

To calculate the probability for the latter two conditions, let us visualize this graphically.

The area of the two triangles together is $$2 * \frac{1}{2} * \frac{1}{4} * \frac{1}{4} = \frac{1}{16}$$ Hence the probability that one line segment is longer than $75$ cm is $$3 * \frac{1}{16} = \frac{3}{16}$$

Part (b)

For these three line segments to form a triangle, the following conditions must be satisfied

$$ X + Y - X > 1 - Y \Rightarrow Y > 1/2 \\ Y -X + 1 - Y > X \Rightarrow X < 1/2 \\ X + 1 - Y > Y - X \Rightarrow Y < X + 1/2 $$

This is for the case assuming $Y > X$. We can write another set of 3 equivalent equations for the case $X >Y$. Visualizing these two feasible regions on a graph, we get

The total area of the shaded figure, and hence the probability that the three line segments form a triangle is

$$2 * \frac{1}{2} * \frac{1}{2} * \frac{1}{2} = \frac{1}{4}$$

Answer 2

Let $X_1$, $X_2$ be the two uniform variables where the breaks happen.

HINTS:

(a) No it's far from $75/100$. One case where the biggest stick is 75 cm long is when both $X_1$ and $X_2$ occur before the 25% mark. The probability this happens is $\mathbb{P}(X_1<0.25 \cap X_2<0.25)=\mathbb{P}(X_1<1/4)\mathbb{P}(X_2<1/4)= 1/16$. What are the other possibilities of values for $X_1$ and $X_2$ that would give a piece of more than 75cm, and what are their probabilities?

(b) Your remarks are correct. Maybe it might be better to wonder in which case the stick cannot form a triangle. In any case, having solved the question (a) will help you greatly.