The following diagram justifies the cosine angle sum rule quite nicely when $0 \alpha, \beta, \alpha + \beta < \pi / 2$.
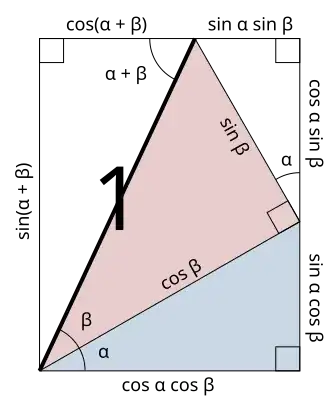
Question: When extending this diagram to the other quadrants (i.e., when $\alpha + \beta > \pi/2$), the argument doesn't seem work anymore, at least not naturally? Am I mistaken? Does there exist a geometric argument for the cosine angle-sum rule for the other quadrants?