Show $ \int_0^\infty\left(1-x\sin\frac 1 x\right)dx = \frac\pi 4 $

Question

How to show that $$ \int_0^\infty\left(1-x\sin\frac{1}{x}\right)dx=\frac{\pi}{4} $$ ?

Answer 1

Use $$ \int \left(1-x \sin\left(\frac{1}{x}\right)\right) \mathrm{d} x = x - \int \sin\left(\frac{1}{x}\right) \mathrm{d} \frac{x^2}{2} = x - \frac{x^2}{2}\sin\left(\frac{1}{x}\right) - \frac{1}{2} \int \cos\left(\frac{1}{x}\right) \mathrm{d}x $$ Integrating by parts again $\int \cos\left(\frac{1}{x}\right) \mathrm{d}x = x \cos\left(\frac{1}{x}\right) - \int \sin\left(\frac{1}{x}\right) \frac{\mathrm{d}x}{x} $: $$ \int \left(1-x \sin\left(\frac{1}{x}\right)\right) \mathrm{d} x = x - \frac{x^2}{2}\sin\left(\frac{1}{x}\right) - \frac{x}{2} \cos\left(\frac{1}{x}\right) + \frac{1}{2} \int \sin\left(\frac{1}{x}\right) \frac{\mathrm{d}x}{x} $$ Thus: $$ \begin{eqnarray} \int_0^\infty \left(1-x \sin\left(\frac{1}{x}\right)\right) \mathrm{d} x &=& \left[x - \frac{x^2}{2}\sin\left(\frac{1}{x}\right) - \frac{x}{2} \cos\left(\frac{1}{x}\right)\right]_{0}^{\infty} + \frac{1}{2} \int_0^\infty\sin\left(\frac{1}{x}\right) \frac{\mathrm{d}x}{x} = \\ &=& 0 + \frac{1}{2} \int_0^\infty \frac{\sin{u}}{u} \mathrm{d} u = \frac{\pi}{4} \end{eqnarray} $$ where the last integral is the Dirichlet integral.

Answer 2

Sasha's answer concisely gets the answer in terms of the Dirichlet integral, so I will evaluate this integral in the same way that the Dirichlet integral is evaluated with contour integration.

First, change variables to $z=1/x$: $$ \int_0^\infty\left(1-x\sin\left(\frac1x\right)\right)\,\mathrm{d}x =\int_0^\infty\frac{z-\sin(z)}{z^3}\,\mathrm{d}z\tag{1} $$ Since the integrand on the right side of $(1)$ is even, entire, and vanishes as $t\to\infty$ within $1$ of the real axis, we can use symmetry to deduce that the integral is $\frac12$ the integral over the entire line and then shift the path of integration by $-i$: $$ \int_0^\infty\frac{z-\sin(z)}{z^3}\,\mathrm{d}z =\frac12\int_{-\infty-i}^{\infty-i}\frac{z-\sin(z)}{z^3}\,\mathrm{d}z\tag{2} $$ Consider the contours $\gamma^+$ and $\gamma^-$ below. Both pass a distance $1$ below the real axis and then circle back along circles of arbitrarily large radius.

$\hspace{4.4cm}$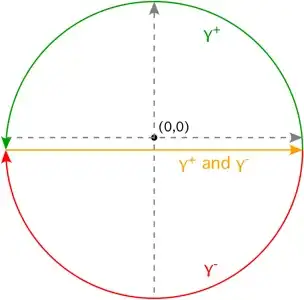

Next, write $\sin(z)=\frac1{2i}\left(e^{iz}-e^{-iz}\right)$ and split the integral as follows $$ \frac12\int_{-\infty-i}^{\infty-i}\frac{z-\sin(z)}{z^3}\,\mathrm{d}z =\frac12\int_{\gamma^-}\left(\frac1{z^2}+\frac{e^{-iz}}{2iz^3}\right)\,\mathrm{d}z -\frac12\int_{\gamma^+}\frac{e^{iz}}{2iz^3}\,\mathrm{d}z\tag{3} $$ $\gamma^-$ contains no singularities so the integral around $\gamma^-$ is $0$. The integral around $\gamma^+$ is $\color{#00A000}{2\pi i}$ times $\color{#00A000}{-\dfrac{1}{4i}}$ times the residue of $\color{#C00000}{\dfrac{e^{iz}}{z^3}}$ at $\color{#C00000}{z=0}$; that is, $\color{#00A000}{-\dfrac\pi2}$ times the coefficient of $\color{#C00000}{\dfrac1z}$ in $$ \frac{1+iz\color{#C00000}{-z^2/2}-iz^3/6+\dots}{\color{#C00000}{z^3}}\tag{4} $$ Thus, the integral around $\gamma^+$ is $\color{#00A000}{\left(-\dfrac\pi2\right)}\color{#C00000}{\left(-\dfrac12\right)}=\dfrac\pi4$. Therefore, combining $(1)$, $(2)$, and $(3)$ yields $$ \int_0^\infty\left(1-x\sin\left(\frac1x\right)\right)\,\mathrm{d}x=\frac\pi4\tag{5} $$ As complicated as that may look at first glance, with a bit of practice, it is easy enough to do in your head.

Answer 3

Let's start out with the variable change $\displaystyle x=\frac{1}{u}$ and then turn the integral into a double integral: $$\int_{0}^{\infty} {\left( {1 - \frac{\sin u}{u}} \right)\frac{1}{u^2}} \ du=$$ $$ \int_{0}^{\infty}\left(\int_{0}^{1} 1 - \cos (u a) \ da \right)\frac{1}{u^2} \ du=$$ By changing the integration order we get $$ \int_{0}^{1}\left(\int_{0}^{\infty} \frac{1 - \cos (a u)}{u^2} \ du \right)\ \ da=\int_{0}^{1} a \frac{\pi}{2} \ da=\frac{\pi}{4}.$$

Note that by using a simple integration by parts at $\displaystyle \int_{0}^{\infty} \frac{1 - \cos (a u)}{u^2} \ du$ we immediately get $\displaystyle a\int_{0}^{\infty} \frac{\sin(au)}{u} \ du = a\int_{0}^{\infty} \frac{\sin(u)}{u}\ du$ that is $\displaystyle a\frac{\pi}{2}$. The last integral is the famous Dirichlet integral.
Hence the result follows and the proof is complete.

Q.E.D. (Chris)

Answer 4

Another way is to use Laplace transform to evaluate this improper integral. In fact, let $f(x)=x-\sin x$ and then $F(s)=\frac{1}{s^2}-\frac{1}{s^2+1}$. Thus \begin{eqnarray*} \mathcal{L}\big\{\frac{f(x)}{x}\big\}&=&\int_s^\infty F(s)ds=-\frac{\pi}{2}+\frac{1}{s}+\arctan s, \\ \mathcal{L}\big\{\frac{f(x)}{x^2}\big\}&=&\int_s^\infty(-\frac{\pi}{2}+\frac{1}{u}+\arctan u)du\\ &=&-1+s(\frac{\pi}{2}-\arctan s)+\ln\frac{\sqrt{s^2+1}}{s}, \\ \mathcal{L}\big\{\frac{f(x)}{x^3}\big\}&=&\int_s^\infty\left(-1+u(\frac{\pi}{2}-\arctan u)-\ln\frac{\sqrt{u^2+1}}{u}\right)du\\ &=&\frac{s}{2}-\frac{\pi s^2}{4}-\frac{1}{2}\arctan s+\frac{1}{2}s^2\arctan s+s\ln s-\frac{1}{2}s\ln(s^2+1). \end{eqnarray*} From this, one can obtain \begin{eqnarray*} &&\int_0^\infty (1-x\sin\frac{1}{x})dx=\int_0^\infty\frac{x-\sin x}{x^3}dx=\lim_{s\to 0^+}\mathcal{L}\big\{\frac{f(x)}{x^3}\big\}\\ &=&\lim_{s\to 0^+}(\frac{\pi}{4}+\frac{s}{2}-\frac{\pi s^2}{4}-\frac{1}{2}\arctan s+\frac{1}{2}s^2\arctan s+s\ln s-\frac{1}{2}s\ln(s^2+1))\\ &=&\frac{\pi}{4}. \end{eqnarray*}

Answer 5

An idea with complex integration. First, we change variables:

$$x=\frac{1}{u}\Longrightarrow dx=-\frac{du}{u^2}\Longrightarrow \int_0^\infty\left(1-x\sin\frac{1}{x}\right)dx=-\int_\infty^0\left(1-\frac{1}{u}\sin u\right)\frac{du}{u^2}=$$

$$=\int_0^\infty\frac{x-\sin x}{x^3}dx$$

Define (with circular paths always in the positive anticlockwise direction)

$$f(z)=\frac{iz-e^{iz}}{z^3}\,\,,\,\gamma_r:=\{re^{it}\;|\;r>0\,,\,0\leq t\leq \pi\}$$

$$\Gamma:=[-R,-\epsilon]\cup\left(-\gamma_\epsilon\right)\cup[\epsilon,R]+\gamma_R$$

We also calculate the residue of the function at $\,z=0\,$ by means of power series:

$$f(z)=\frac{iz-e^{iz}}{z^3}=\frac{1}{z^3}\left[iz-\left(1+iz-\frac{z^2}{2}-\frac{iz^3}{6}+...\right)\right]=\frac{1}{z^3}\left(-1+\frac{z^2}{2}+..\right)=$$

$$=-\frac{1}{z^3}+\frac{1}{2z}+...\Longrightarrow\operatorname{Res}_{z=0}(f)=\frac{1}{2}$$ We use the above, and the lemma and its corollary in the answer here , to get:

$$\lim_{\epsilon\to 0}\int_{\gamma_\epsilon}f(z)\,dz=\frac{\pi i}{2}$$

We also have

$$\left|\int_{\gamma_R}f(z)\,dz\right|\leq\max_{z\in\gamma_R}\frac{|iz-e^{iz}|}{|z^3|}R\pi\leq \max_{z=Re^{it}}\frac{R+e^{-R\sin t}}{R^2}\pi\xrightarrow [R\to\infty]{}0$$

(Note: $\sin t\geq 0\,$ when $\,t\in [0,\pi]\,$)

Thus, by Cauchy's Formula and the above, and since $\,f(z)\,$ is analytic in the domain enclosed by $\,\Gamma\,$:

$$0=\int_\Gamma f(z)\,dz=\int_{-R}^\epsilon f(x)\,dx-\int_{\gamma_\epsilon}f(z)\,dz+\int_\epsilon^R f(x)\,dx+\int_{\gamma_R}f(z)\,dz$$

And passing now to the limits when $\,\epsilon\to 0\,\,,\,\,R\to \infty\,$ , we get

$$0=\int_{-\infty}^\infty\frac{ix-e^{ix}}{x^3}-\frac{\pi i}{2}\stackrel{\text{equalling imaginary parts}}\Longrightarrow \int_{-\infty}^\infty\frac{x-\sin x}{x^3}=\frac{\pi}{2}$$

And since the integrand is an even function, we finally get

$$\int_0^\infty\left(1-x\sin\frac{1}{x}\right)dx=\int_0^\infty\frac{x-\sin x}{x^3}dx=\frac{\pi}{4}$$