concatenating translation and rotation matrix - what am I doing wrong?

Question

I'm teaching myself linear algebra trying to write a 3D script. Mostly relying on Khan Academy for revising math itself, and supplementing with 3D graphics blogs, websites, etc.

I got as far as using matrix multiplication to perform compound rotations (say in 3 axes, depending on 3D package's convention for rotation order), but now I'm trying to understand concatenating a rotation and a translation.

I did this example in 2D (3D homogeneous space) for simplicity of graphing.

Working from Wikipedia (Translation: Matrix representation [see disclaimer at bottom]) I understand I need to convert my vectors to homogeneous space with w = 1, and multiply by the translation matrix T.

This works for only translation (T) and for rotation*translation (R * T). But produces garbage for T * R. As you can see in my graph and calculations, I would expect A' = TRA somewhere around [0.3,6] point but it is not.

What am I missing? I'd appreciate pointing me in the right way.

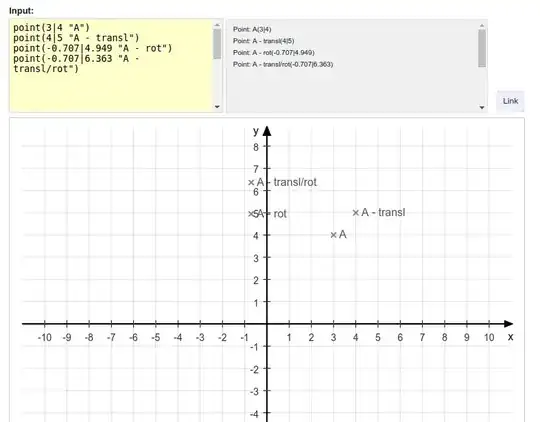
(^In afterthought: I labelled operations in the order of reading, so "A - transl/rot" is technically actually: R * T * A )

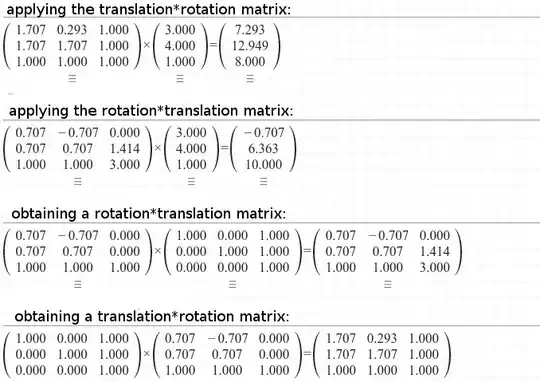
Many Thanks.

There is a way to combine rotation and translation in one matrix, but it relies on a trick using $4\times 4$ matrices (rather than just the $3\times 3$ matrix for the rotation alone). I've explained the trick before in an answer. Let me try and dredge it up. — hardmath, Aug 25 '16 at 12:06
Closely related: How to multiply vector 3 with 4by4 matrix, more precisely position*transformation matrix. — hardmath, Aug 25 '16 at 12:11
Not sure it's answer-worthy, but I was now able to get a correct result by using a bottom row of zeroes instead of ones in my Rotation matrix - i.e. element r_31 = 0 and r_32 = 0. My previous (erroneous) rationale being that each column of the R matrix is like a vector (a transformed basis vector) so should have w=1. — DailyFrankPeter, Aug 25 '16 at 13:38
I think your problem lies in what you've called "a rotation matrix". The matrix that represents a rotation should be orthonormal, but yours is not (because the bottom row is not orthogonal to the top rows, and does not have length one). — hardmath, Aug 25 '16 at 17:26
@hardmath, yes that was the problem (i.e. the bottom row). Can one speak of "orthonormality" in projective (homogenous) space, though? That's what the bottom row (and last column) is. Only r_11, r_12, r_21, r_22 come from an orthonormal basis (of 2D space). — DailyFrankPeter, Aug 28 '16 at 16:28

score 2 · Answer 1 · answered Jun 22 '19 at 03:18

If you want to rotate and translate a 2D point $p=[x,y]^T$, then this can be written $$ q = Rp + t $$ where $t=[t_x,t_y]^T$ and $R\in SO(2)$ as a $2\times 2$ matrix.

To put this as a matrix multiplication, notice that $$ \underbrace{ \begin{bmatrix} q \\ 1 \end{bmatrix}}_{q_h} = \underbrace{ \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}}_{M} \underbrace{ \begin{bmatrix} p \\ 1 \end{bmatrix}}_{p_h} $$ simply as a fact of linear algebra. This can be interpreted as moving $p$ to homogeneous coordinates $p_h$, and then constructing $M$ by appending $t$ to it (after moving $t$ to homogeneous coordinates). From a geometric perspective, why must we place zeros underneath $R$ (which is the solution you discovered)? It is because we need the last element of $q_h$ (say $a$) to be $1$, else we would be moving (scaling) $q$ by $a$ in real space!

PtH · Answer 2 · 2019-06-22T06:27:53.183

There are deeper points here that are worth noting:

Translation is not a linear transformation. Hence it cannot be written as a multiplication by a matrix (unless one uses clever tricks).
Rotating and then translating will give different results to translating and then rotating.

Proof that translation is not linear: Define $T(x)$ as the transformation that translates the point $x$ by a displacement $b$. Then $T(x) = x + b$ for any point $x$. Now suppose that $T$ is a linear transformation. Then by definition we must have $T(x+y) = T(x) + T(y)$ for all $x$ and $y$. Now $T(x+y) = x+y + b$ but $T(x) + T(y) = x+b + y+b = x+y + 2b$ so we have equality for all $x$ and $y$ if and only if $b=0$.

Reference that $T(x)$ is a linear transformation (on a finite-dimensioned vector space) if and only if $T(x) = Ax$ for some matrix $A$: Wolfram and it is also a common student exercise.

concatenating translation and rotation matrix - what am I doing wrong?

2 Answers2