Normal vectors of hedrons

Question

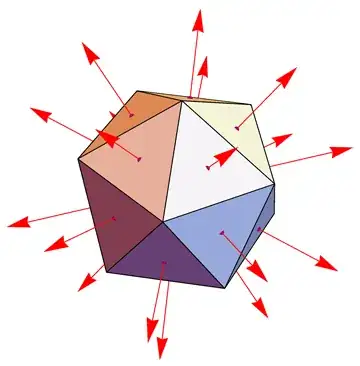
I am trying to quantize the normal vectors I obtain into several bins. To do that, I will compute the dot product of the normal vector with a predefined set of vectors and take the maximum.

My question is: How do I determine the normal vectors of $3D$ shapes for example, an Icosahedron with $20$ faces ? Also, it would help a lot if someone tells me a shape that has normal vectors going in the $x, y, z, xy, xz, yz$.

What I mean by $xy$ would be it is $45^\circ$ (cutting the $xy$ plane diagonally).

Answer 1

For the specific case of an icosahedron, the face normal vectors pass through the centroid of each triangle:

---

 

---

For other polyhedra, use the cross-product to construct the normals.