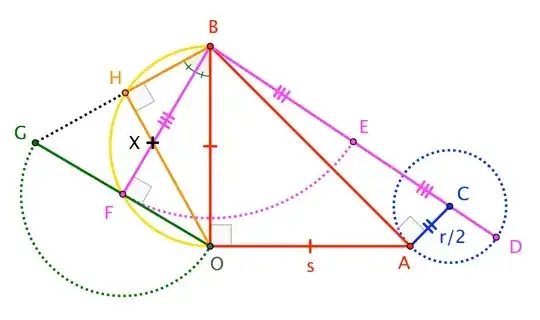
Given two lengths $\overline{AB} = R$ and $\overline{AE} = r$ with $R > r$, how to construct a right triangle $\triangle ABC$ with a hypotenuse $\text{length} = R$ and the length of the $\text{bisector} = r$ as shown below in the figures?
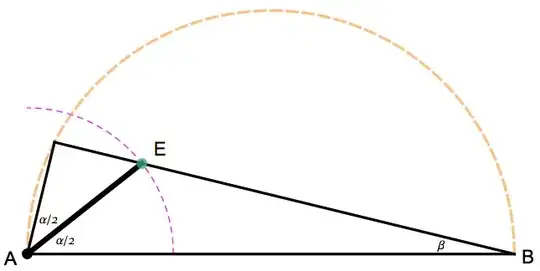 Somehow I cannot get the label working for vertex $C$, the one on the orange circle, sorry.
Somehow I cannot get the label working for vertex $C$, the one on the orange circle, sorry.
The right triangle $\triangle ABC$ has the angles $\alpha + \beta = \pi/2$, where $\angle ACB$ is the right angle.
The bisector $\overline{AE}$ splits $\angle CAB = \alpha$ into two.
The figure above shows the case for a relatively smaller $r$ (magenta) compared with $R$ (orange), and the figure below is for a relatively large $r$.
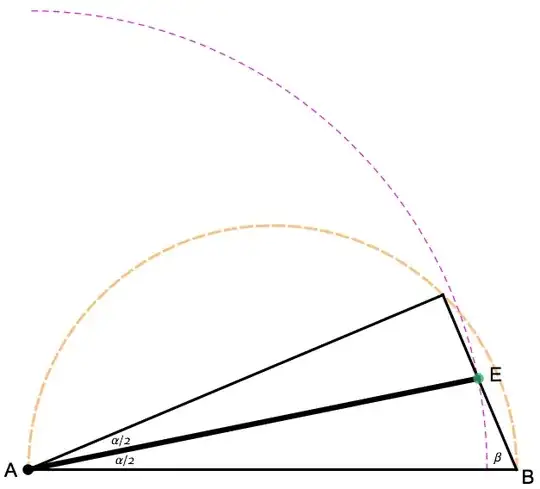
As an analytic-geometry problem, I have been able to solve the coordinates $(x_E, y_E)$ of point $E$ (taking e.g. point $A$ as the origin), but I cannot tell from this expression if there's a sensible compass-and-straightedge construction:
$$ x_E = \frac{r}{4R} \left( r + \sqrt{ r^2 + 8R^2} \right) \qquad \text{or equivalently} \qquad \cos \frac{\alpha}2 = \frac{1}{4R} \left( r + \sqrt{ r^2 + 8R^2} \right)$$
As of now I'm trying to understand the content of some related post here on StackExchange; upon first glance it seems considerable work is needed to make their results helpful for my case.
btw, this construction is related to the L'H$\hat{o}$pital's weight (pulley) problem (in calculus).