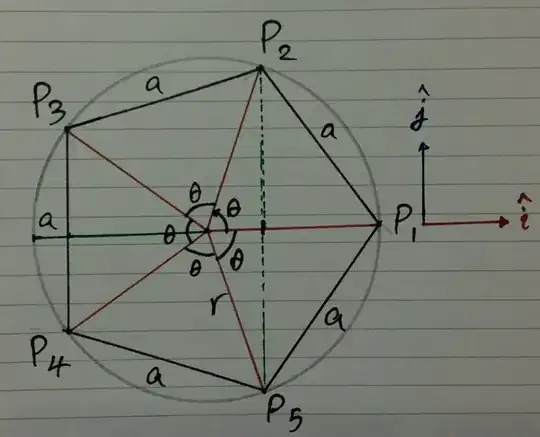
[INTRO]
In such arrangement of identical charged particles named $P_1$, $P_2$, ..., $P_n$ (In this diagram $n=5$), the electric field in the center is always zero.
The electric field is given by this equation:
$$\vec F=k\frac{q}{r^2}\hat r$$
Where $\hat r$ points to the radial direction.
If $2|n$, then the forces are obvious canceled by symetry.
If $n$ is odd, again the components of forces in the $y$ axis cancel by symetry. But for the $x$ direction the components cancel if this condition is true:
$$\sum_{c=0}^{n-1}\cos(c \theta)=0 \ \ \ \ \ \ \theta=\frac{2\pi}n$$
[END OF INTRO]
My main problem is to prove for any $n$, this relation holds:
$$\sum_{c=0}^{n-1}\cos(2\pi \frac{c}{n})=0$$