1

I'm trying to get a grasp on the differentials concept and I arrived to this conclusion, but I'm not sure it's correct since I haven't found exactly this way of defining them anywhere.

I'm pasting a picture of my notes because I'm not sure how to express this otherwise.

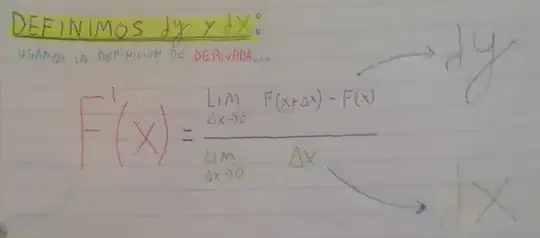
Pic of my notes

From my understanding, defining $dx$ and $dy$ this way gives me the following properties:

  • Differentials are limits, not numbers, so they must be dealt with using algebra of limits
  • Differentials represent infinitesimal quantities

I want to check if these deductions are correct, misguided or maybe plain wrong.

Zev Chonoles
  • 129,973
Joaquin Brandan
  • 705

1 Answers1

2

I don't see any definitions of $dx$ and $dy$ there. There are ways of defining differentials $dx$ and $dy$, but it's not as limits of $\Delta x$ and $\Delta y$. You might look at this question and its answers.

Community
  • 1
Robert Israel
  • 448,999
  • So the fact that a derivative can be defined as the quotients of limits of $ Δ x$ has nothing to do with the notation $dx/dy$ ? – Joaquin Brandan Aug 19 '16 at 21:29
  • It only has to do historically. "Differentials" are disgusting things to introduce in a first calculus course. – YoTengoUnLCD Aug 19 '16 at 21:35
  • Is it bad to interpret them in this way until i gain a better understanding of mathematics where i can understand Differentials with more rigor?

    would this lead me to errors in practical applications of calculus, or while interpreting calculus books?

     – Joaquin Brandan Aug 19 '16 at 21:44
  • @JoaquinBrandan Y... Es medio difícil de decir. Muchos profesores, especialmente en física van a usar argumentos con "diferenciales" para explicar conceptos, sin siquiera ellos saber que son realmente (como mucho te dirán "son números muy chiquitos!"). Es por esta razón que siempre odie que siquiera introduzcan esta notación para la derivada. Cuando estudies más matemática (si es que estas estudiando algo como licenciatura en matemática), en algún momento vas a ver formas diferenciales, que clarifica un poco más estos conceptos, pero no te apresures. – YoTengoUnLCD Aug 20 '16 at 03:12
  • Y cada vez que hagan cosas como "multiplicar diferenciales", tómalo con pinzas (creo que la mejor interpretación que se le puede dar a $dy/dx$ en este punto es como un solo símbolo (no $dy$ dividido por $dx$, tal como $\log x$ no es $l\cdot o\cdot g \cdot x$ : )). Saludos. – YoTengoUnLCD Aug 20 '16 at 03:14