Aka there might be a simple name for that question, but here goes:
So I'm trying to score objects on certain parameters, one of which is price. The way I calculate the score is I multiply each parameter together. Pretty simple stuff.
Ex: score = Param1 * Param2 * Param3 * Param4 * price
Each parameter could individually be assigned an exponent (ranging from 0.5 to 3.5 to give it more or less weight in the equation). I do not know if that influences the complexity of what I am asking for.
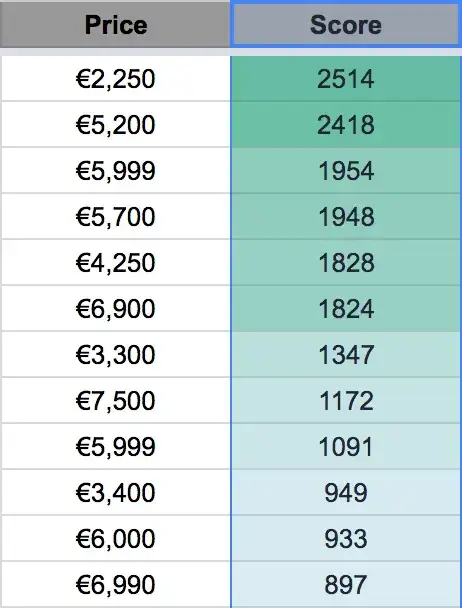
Now, I have an ordered list where items are filtered from descending score. All parameters are set in stone, but price might vary; each item's price could potentially be discussed.
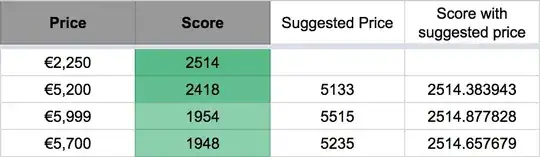
What I'm trying to do is to suggest a bargained price for each item so it matches the item with the highest score.
For the moment, those 3 suggested prices have been manually found (and aren't very accurate of course).
The idea is that basically, an item might be worth giving priority over a higher ranked item if we can manage to bargain a good price. We're on the buyer side, so better score means cheaper price.
So the final question is: what equation(s) do I need to come up with to find a price whose score would match the best score ?
Edit: I should've explained things a bit more clearly, sorry about that. I thought the following wouldn't have any impact on what I was asking, but it does seeing the answers.
Turns out I misled the question by withholding some information regarding the parameters; they are all composites, ranging from 0 to positive infinite. The way I calculate them is based on certain criteria so that they don't go too far off the 0.5 - 2.5 range. This holds true for the price parameter as well. If it goes above a certain threshold, I return the following value:
$\left(\frac{threshold}{price}\right)^5$
Given a threshold of $5000$ and a price of $5700$, the returned value will be $0.88$. The 5th exponent is there to make each dollar above the threshold have a more dramatic effect on the total score.
On the other hand, if the price is below the threshold, the composite is calculated in the following manner:
$\frac{threshold}{price}$
So either a parameter increases the score, or it decreases it slightly (since they're all multiplied between each other).
As an example, here's the formula with the item with the highest score's parameters:
$1.5 * 1.99 * 450.00 * 1.44 * 1.18 = 2272$
And one with a lower score (due to the item's higher price):
$2.00 * 2.92 * 350.00 * 1.00 * 0.88 = 1790$
As you can see, it could've score higher if it weren't for its steeper price. That's why I'm trying to find a formula that suggest a price to make the item worth it. So as the buyer, you could try and discuss to get to that price.