-4

Prove that:- Any group of order 4 is either cyclic or isomorphic to Z2*Z2 where Z2 is residue group of natural numbers modulo 2.

Sanket yadav
  • 1
  • Try to write the multiplication table for a group of order 4. – Sachchidanand Prasad Aug 13 '16 at 05:13
  • 2
    @SachchidanandPrasad, in my opinion, this approach doesn't help understand the structure of the group. – avs Aug 13 '16 at 05:16
  • It will. Because there can only be two possible tables, one will correspond to cyclic and other will correspond to the other part. – Sachchidanand Prasad Aug 13 '16 at 05:18
  • See also: http://math.stackexchange.com/questions/165341/any-group-of-order-four-is-either-cyclic-or-isomorphic-to-v http://math.stackexchange.com/questions/443642/prove-that-every-group-of-order-4-is-abelian http://math.stackexchange.com/questions/702384/suppose-g-is-a-group-of-order-4-show-either-g-is-cyclic-or-x2-e – Martin Sleziak Aug 13 '16 at 08:04

3 Answers3

1

We prove every group $G$ of order $p^2$ is either cyclic or isomorphic to $\mathbb Z_p\times \mathbb Z_p$

first we prove it is abelian, this is an immediate consquence of these three lemmas:

lemma $1$: If $\frac{G}{Z(G)}$ is cyclic then $G$ is abelian.

lemma $2$: the center of a finite $p$-group is not trivial.

lemma $3$: a group of prime order is cyclic.

Once we know it is abelian there are two cases:

case $1$: $G$ has an element of order $p^2$, and hence is cyclic

case $2$: $G$ has no element of order $p^2$, hence by Lagrange's theorem all of its non identity elements have order $p$. take an element $g$ of order $p$ and then take a second element $h\in G\setminus \langle g \rangle $ with order $p$. We have $|\langle g \rangle \langle h \rangle |=\frac{|\langle g \rangle | |\langle h \rangle |}{|\langle g \rangle \cap \langle h \rangle | }$. Clearly the denominator is $1$ by lagrange's theorem, so these two subgroups are both normal, their intersection is trivial and their product is all of $G$. This implies $G\cong \langle p \rangle \times \langle q\rangle \cong \mathbb Z_p\times \mathbb Z_p$

Asinomás
  • 105,651
1

Let the group is $$G=\{e,a,b,c\}.$$ From Lagrange's theorem, the order of each element will divide 4. So, order fo any element will be either 2 or 4. If it is 4 then the group is cyclic. If for each element of the group $G$ order is 2 then it is isomorphic to $\mathbb{Z}_2\times \mathbb{Z}_2.$

We will prove 2nd part by showing that any two non-cyclic groups of order 4 are isomorphic to each other. For this, let us take any two non-cyclic groups of order 4, denote them by $ G $ and $ G^\prime $. Let $ e $ and $ e^\prime $ denote the identity of these groups respectively. Let $$ G=\{e,x,y,z\} $$ and $$G^\prime=\{e^\prime,x^\prime,y^\prime,z^\prime\}.$$ We must have $ x^2=y^2=z^2=e,\ (x^\prime)^2=(y^\prime)^2=(z^\prime)^2=e^\prime $. 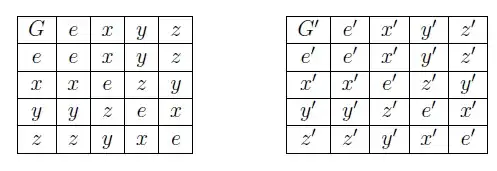enter image description here

It is clear from the table that the map $$ \phi\ :\ G\to G^\prime $$ given by \begin{align*} \phi(e)& =e^\prime\\ \phi(x) & = x^\prime\\ \phi(y)& = y^\prime\\ \phi(z) & = z^\prime\ \text{is an isomorphism.} \end{align*}

Sachchidanand Prasad
  • 2,770
0

Say you have a group of order 4. If it has an element of order 4, the group is cyclic.

Otherwise, every non-identity element has order 2 (this is because, by Lagrange's theorem, the order of an element must divide the order of the group). Therefore, each element except the identity has order 2, so the group is abelian. Now you can look here: Group where every element is order 2

Community
  • 1
avs
  • 6,276