How can I find all solutions to differential equation?

Question

How one can find all functions $f$ that there exists $f'$ satisfying $(f(x))^2+(f'(x))^2=1$? I just found solutions $f(x)=1,-1,\sin x$.

Answer 1

We are going to obtain in two steps all $C^1$ solutions of

$$\tag{0}(f(x))^2+(f'(x))^2=1.$$

Step 1: Let us follow a method similar to that given either by @David Quinn for example or @Ian Eerland or @Battani, with some supplementary precision on the intervals of validity.

Let $f$ be a solution to $(0)$.

Let us consider a point $x_0$. Either

• case 1: $|f(x_0)|=1$ or

• case 2: $|f(x_0)|<1$, which implies $|f'(x_0)|>0$.

Let us detail case 2.

By continuity of $f$, there exist $\epsilon_1>0$ such that on $I_1:=(x_0-\epsilon_1,x_0+\epsilon_1)$ we have $|f(x)|<1$.

By continuity of $f'$, there exist $\epsilon_2>0$ such that on $I_2:=(x_0-\epsilon_2,x_0+\epsilon_2)$ we have $|f'(x)|>0$.

Let us transform $(0)$ into

$$\tag{1}\dfrac{y'}{\sqrt{1-y^2}}=s$$

Differential equation (1) needs to be considered for values of variable $x$ in $I:=I_1 \cap I_2$ in order that the ratio is well defined and that the sign $s=\pm1$ doesn't change throughout this interval $I$.

Taking a primitive function on $I$ of both sides of (1):

$$\arcsin(y)=s x+\varphi \ \ \ \text{for some constant} \ \varphi.$$

Thus $y=f(x)=\sin(s x+ \varphi)$ on interval $I$ with either $s=1$ or $s=-1$.

This solution can be presented under the simpler form: $f(x)=\sin(x+ \varphi)$ (one finds back case $s=-1$ through replacement of $\varphi$ by $\varphi+\pi$).

Conclusion of step 1: a solution $f$ and a particular point $x_0$ being given, there are two cases:

\begin{cases} (a) \ \text{Either} \ f(x_0) = \pm1 \ \text{or}\\ (b) \ \text{There exist an interval} \ J \ \text{containing} \ x_0 \ \text{ such that,} \forall x \in J, \ f(x)=\sin(x+\varphi) \ \end{cases}

for a certain $\varphi$ ($J$ being any interval of validity of solution $f$, including interval $I$ as defined before).

Step 2: We are going to obtain these intervals $J$ by using a topological argument (A recall about topology can be found there). From (0), we know that the values taken by $f(x)$ are in the closed interval $[-1,1]$. Now consider the set of values of $x$ such that their image is in the open interval $(-1,1)$:

$$S:=\{x \ | -1<f(x)<1 \}=f^{-1}((0,1)). $$

$S$ is an open set, being the preimage of an open set by a continuous function; as such, it can be written as a countable union of open intervals $S=\bigcup_k (a_k,b_{k})$ (see this). In this way ;

(b) will be valid on open intervals $(a_k,b_k)$

(a) will be valid on closed intervals $[b_k,a_{k+1}]$.

At junction point $b_k$, the only possible way to preserve $C^1$ continuity is by taking, according to the value of $\lim_{x\rightarrow b_k} f(x)$ value $1$ or $-1$ for the whole closed interval $[b_k,a_{k+1}]$. Same procedure at the initial junction point $a_k$.

Let the curve of $y=sin(x)$ restricted

• to $[0,\pi/2]$ (increasing) be called an $s_+$ arc.

• to $[\pi/2,\pi]$ (decreasing) be called an $s_-$ arc.

Let a line segment of any positive length with equation $y=1$ (resp. $y=-1$) be called a $1_+$ (resp a $1_-$).

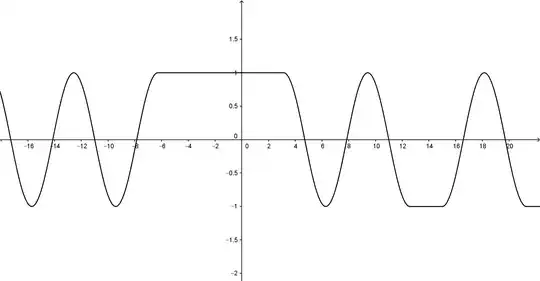
Thus one can describe the possible $C^1$ integral curves of (0) by a $C^1$ "glueing" of curves as a (finite or infinite) repetition of the following "motives":

$$\cases{1_+^*[s_-1_-^*s_+1_+^*]^*\\(1_-)^*[s_+1_+^*s_-1_+^*]^*}$$

(mathematical "grammars" notations, where exponant * means 0 or more times). See figure.

• Intervals where the solution is constant may have any length.

• "Phase shifts" $\varphi_k$ of the sine curves are specific to each interval.

• It is to be noted that closed intervals $[b_k,a_{k+1}]$ can be reduced to a point.

Appendix : I had, at first, obtained a certain family of solutions by differentiating both sides of $(0)$:

$$2f'(x)(f(x)+f''(x))=0.$$

After a certain number of hours spent on this method, which assumes $f \in C^2$, I realized that it is impossible to go back to the initial equation dealing with $C^1$ solutions.

Added on August 30th: this differential geometry question gives an application of (0).

Answer 2

If $y=f(x)$, you have $$\frac{dy}{dx}=\pm\sqrt{1-y^2}$$ Either $y=\pm 1$, or if $y\neq \pm 1$, $$\Rightarrow\int\frac{1}{\sqrt{1-y^2}}dy=\pm x+c$$ $$\Rightarrow y=\sin(\pm x+c)$$

Answer 3

$$f(x)^2+f'(x)^2=1\Longleftrightarrow$$ $$f'(x)^2=1-f(x)^2\Longleftrightarrow$$ $$f'(x)=\pm\sqrt{1-f(x)^2}\Longleftrightarrow$$ $$\frac{f'(x)}{\sqrt{1-f(x)^2}}=\pm1\Longleftrightarrow$$ $$\int\frac{f'(x)}{\sqrt{1-f(x)^2}}\space\text{d}x=\int\pm1\space\text{d}x\Longleftrightarrow$$

---

For, the integral on the LHS substitute $u=f(x)$ and $\text{d}u=f'(x)\space\text{d}x$:

$$\int\frac{f'(x)}{\sqrt{1-f(x)^2}}\space\text{d}x=\int\frac{1}{\sqrt{1-u^2}}\space\text{d}u=\arcsin(u)+\text{C}=\arcsin(f(x))+\text{C}$$

For, the integral on the RHS:

$$\int\pm1\space\text{d}x=\pm\int1\space\text{d}x=\pm x+\text{C}=\text{C}\pm x$$

---

$$\arcsin(f(x))=\text{C}\pm x$$

Your solutions, can be found by setting $\text{C}$, when we have $f(a)=b$:

$$\arcsin(b)=\text{C}\pm a\Longleftrightarrow\text{C}=\arcsin(b)\mp a$$

So:

$$\arcsin(f(x))=\left(\arcsin(b)\mp a\right)\pm x$$

Answer 4

$$ y^2+y^{\prime^2}=1 $$

Differentiate to get

$$ 2 y y^{\prime} + 2 y^{\prime} y^{\prime \prime } =0$$

Factorize, two different/separate solutions

$$ y^{\prime} = 0 , \quad y = C $$

$$ y^{\prime \prime } + y = 0, $$

with particular solution non-homogeneous DE

$$ y = A \sin (x + B) +1 $$

First solution

$$ C= 1, \quad \rightarrow y=1 ; $$

For second solution when plugged into given equation $ B=0, A=1$,

so that only $ y= 1+ \sin x $ is admissible.

EDIT1

Squaring introduces extraneous solutions. But how an elementary direct solution got missed!

$$ y^2+y^{\prime^2}=1 ,\quad y^{\prime }= \pm \sqrt{1-y^2} $$

$$\pm \dfrac{dy}{\sqrt{1-y^2}}= dx $$

$$\pm \int\dfrac{dy}{\sqrt{1-y^2}}= x +C = \pm \sin^{-1}y $$

$$ y = \pm \sin(x+C) $$

which includes all solutions.

CHECK: $ \, y^{\prime} = \pm \cos(x+C),\quad y^2+y^{\prime^2}=1. $

and it includes both the envelopes mentioned by OP:

$$ y= \pm 1 $$

And I believe this envelope solution aspect of differential equations theory is often discarded as being trivial, which definitely it is not.

Answer 5

$$(f(x))^{ 2 }+(f'(x))^{ 2 }=1\\ { y }^{ 2 }+{ \left( y\prime \right) }^{ 2 }=1\\ y\prime =\pm \sqrt { 1-{ y }^{ 2 } } \\ \int { \frac { dy }{ \sqrt { 1-{ y }^{ 2 } } } =\pm \int { dx } } \\ \arcsin { y } =\pm x+C\\ y=\sin { \left( \pm x+C \right) } $$