1

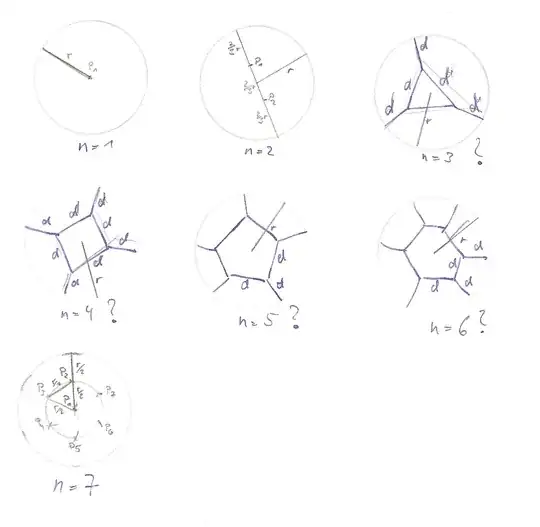
There is a finite, circular area $A=\pi \times r^2$ with a given radius $r$ and a variable number of points $P_n$ ($n \in \mathbb{N}_{>0}$) that are to be placed inside of this area.

What is the distance $d$ to the closest dots when placing them in a way to maximise this closest distence while also placing them at minimum the same distance $d$ to the edge of the area?

This is distinct from this and similar problems by trying to also maximise the distance between the edge and points and the points at the same time while also using $n$ points instead of 2.

For $n=1$ the obvious solution is $d=r$ while $P_1$ is also the center of the circle.

For $n=2$ I get a distance of $d= r \frac{2}{3} $ from the simple geometry: They have to be on the opposite sides of the center of the circle, so they are both on a line of $ 2 \times r$, which they divide into 3 areas of equal length.

For $n=3$ to $n=6$ I lack a good formula, but I think the solution might be to place them on polygons with a number of corners equal to $n$.

For $n=7$ I found, that one of the points has to end up in the center of the circle, while the other 6 form a hexagon around it, that should have a side length of $d=\frac{r}{2}$. I derived this from experimental drawings, using a set of 7 circles of $R=\frac{r}{2}$ that have their centers always on the edge of 3 others

Is there any formula for the needed distance $d$ for any $n \in \mathbb{N}$? For clarification a sketch: Sketch of cases n=1 to 7

Community
  • 1
Trish
  • 222
  • The sentence "What is the average distance $d$ between these dots when trying to place them as far away from each other while also enforcing that same distance $d$ to the edge of the area?" makes it clear that you don't have a clear picture of the envisaged random situation. – Christian Blatter Aug 09 '16 at 17:43
  • oh, made an errror there - I meant an even distribution. It is not a random distribution problem at all. – Trish Aug 09 '16 at 18:09
  • You haven't defined "evenly distributed". I get the impression that you don't acutally mean anything by that other than the maximisation of $d$ that you describe further down; if you so, it should be deleted to avoid confusion. – joriki Aug 09 '16 at 18:23
  • It's a lot clearer now, but the expressions "the distance $d$ between the dots" and "placing them at maximum distance" are a bit unclear -- there are many pairs of dots, and they're not all at one and the same distance. It think what you want is to maximise the minimal distance between any pair of points (including boundary points)? – joriki Aug 09 '16 at 18:37
  • 2
    I think you're looking for circle packing in a circle. See Packomania for the best known packings up to $n=2600$. –  Aug 09 '16 at 18:38
  • oh, that's almost what I look for, just... I need the inner radii. However, it seems I encountered a problem that no perfect solution exists as a single yet by trying to calculate the distance that cities would have when plaved with maximum distance to each other and the borders when calculating some fictional country for a P&P game... If you make that a full answer, you get the star. – Trish Aug 09 '16 at 18:59

1 Answers1

2

A simple bound is provided by a circle-packing argument. Assuming that $n$ points $P_1,\ldots,P_n$ can be placed inside a unit circle $\Gamma$ in such a way that $d(P_i,P_j)\geq d$ and $d(\Gamma_i,\Gamma)\geq d$, the $n$ circles $\Gamma_1,\ldots \Gamma_n$ with radius $\frac{d}{2}$ having their centres at $P_1,\ldots,P_n$ are disjoint and they all lie inside a circle with radius $1-\frac{d}{2}$. It follows that: $$ n\cdot \pi\left(\frac{d}{2}\right)^2 \leq \pi\left(1-\frac{d}{2}\right)^2, $$ hence: $$ d\leq 2\frac{\sqrt{n}-1}{n-1} $$ and it is expected that for large $n$ the wanted distance $d$ behaves like $\color{red}{\large\frac{C}{\sqrt{n}}}$ with $C$ being a constant not too far from $2$.

To find almost-optimal arrangements we may just consider an hexagonal tiling, find a circle that encloses $n$ vertices of that tiling and scale everything back.

Jack D'Aurizio
  • 353,855