I’ll sketch out an approach to solving this that can involve some messy algebra, but is conceptually straightforward. It uses some ideas and results from this paper by Alan Horwitz.
Begin by solving the simpler problem of finding an ellipse that’s tangent to the coordinate axes at $(1,0)$ and $(0,1)$. The solution is, of course, not unique: there’s a family of ellipses with these tangents.
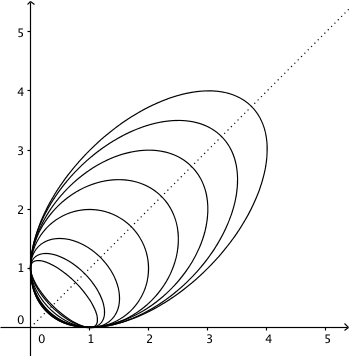
Besides the two tangents, these ellipses share some other features. Their centers all lie on the line $x=y$ and each ellipse is circumscribed by the square $[0,s]\times[0,s]$ for some unique $s>1$. We can thus take this $s$ as a parameter, which yields the following equation for the corresponding ellipse: $$sx'^2+sy'^2-2(s-2)x'y'-2s(x'+y')+s=0.\tag{1}$$ By symmetry, it’s easy to see that the center of the ellipse is at $\left(\frac s2,\frac s2\right)$ and with a bit of work one can calculate that the eccentricity is $\sqrt{s-2\over s-1}$ for $s\ge2$ and $\sqrt{2-s}$ for $1\lt s\le2$. The case $s=2$, of course, produces a circle. Note also that for $s\gt2$, the major axis lies along $x=y$, while for $s\lt2$ the minor axis is along this line.
To solve the general case, one need only apply an affine transformation to one of these ellipses. We’re given $P_1$ on the tangent line $\ell_1$ and $P_2$ on $\ell_2$. Assume in addition that $\ell_1\nparallel\ell_2$. Let $P_0$ be the intersection of the two lines, and let $T$ be the affine transformation that makes the following mappings: $$\begin{align}(0,0)&\mapsto P_0\\(1,0)&\mapsto P_1\\(0,1)&\mapsto P_2.\end{align}$$ This transformation maps ellipses from the constructed family to ones that are tangent to $\ell_1$ at $P_1$ and to $\ell_2$ at $P_2$. The bounding squares are mapped to parallelograms defined by $P_0$, $P_0+s(P_1-P_0)$ and $P_0+s(P_2-P_0)$. That is, the parallelogram has a vertex at $P_0$ and sides that lie along $\ell_1$ and $\ell_2$ with lengths equal to the corresponding line segments scaled by a factor of $s$. This parallelogram circumscribes the image of the ellipse for the same value of $s$.
Thus, even in the general case, $s$ makes sense as a linear “size” parameter for the resulting ellipse. Note that, although $T$ preserves the center, bounding parallelogram and tangent points, it does not preserve the major and minor axes of the ellipse. (The center of the ellipse coincides with the center of the parallelogram, so “eyeballing” it will likely result in inconsistent constraints: these centers all lie along the image of $x=y$, the line through $P_0$ and the opposite corner of the parallelogram.)
Determining the affine map $T$ is almost trivial. In homogeneous coordinates, it can be represented by the matrix $$M=\begin{bmatrix}\mid&\mid&\mid\\P_1-P_0&P_2-P_0&P_0\\\mid&\mid&\mid\end{bmatrix}=\begin{bmatrix}x_1-x_0&x_2-x_0&x_0\\y_1-y_0&y_2-y_0&y_0\\0&0&1\end{bmatrix}$$ which encodes the mapping $$\begin{align}x&=(x_1-x_0)x'+(x_2-x_0)y'+x_0\\y&=(y_1-y_0)x'+(y_2-y_0)y'+y_0.\end{align}$$ Make the appropriate substitutions in equation (1) to get an equation for the mapped ellipse. Depending on how you’re doing this, it might be easier to work with another form of the equation, such as the vector form $(\mathbf x-\mathbf p)^TA(\mathbf x-\mathbf p)=1$, where $\mathbf p$ is the center of the ellipse and $A$ is a positive definite matrix.
If you don’t want to fiddle with an extra parameter, a plausible choice is the ellipse with minimum eccentricity. I haven’t looked at this in enough detail to prove it (the paper I cited proves something similar), but I believe this occurs when the source ellipse also has minimal eccentricity, which is obviously at $s=2$ when it’s the circle $(x'-1)^2+(y'-1)^2=1$.
If $\ell_1\parallel\ell_2$, the situation is a bit different. Now, the center of the ellipse is fixed at the midpoint of $\overline{P_1P_2}$ and what varies is the width of the circumscribed parallelogram. I’ll leave this case for you to work out yourself. It might even be possible to combine the two cases by working entirely in homogeneous coordinates.
Another possibility that I’ll sketch out here is to use “Plücker’s mu.” The idea is to construct two specific conics $Q$ and $Q'$ that satisfy the constraints. Every linear combination $\lambda Q+\mu Q'$ of these conics also satisfies those constraints. Given a point $\mathbf p$ that’s not one of our two fixed points, the unique conic of this family that also passes through $\mathbf p$ is $(\mathbf p^TQ\mathbf p)Q'-(\mathbf p^TQ'\mathbf p)Q$. For one of these generating conics you can take the degenerate conic $\mathbf l_1\mathbf l_2^T+\mathbf l_2\mathbf l_1^T$ that consists of the two tangent lines. A computationally convenient choice for the other conic is the unique parabola with the given tangents. If we set $\mathbf p_0$ to the intersection of the two lines, then this parabola is given in parametric form by the quadritic Bézier curve $(1-t)^2\mathbf p_1+2t(1-t)\mathbf p_0+t^2\mathbf p_2$. You can convert this into Cartesian form using the formula given here, and from there extract the coefficients to form the matrix of the parabola.
It might seem like you end up with two degrees of freedom this way, but you can restrict $\mathbf p$ to a ray that originates at $\mathbf p_0$ and lies “between” the tangents and still generate all of the possible ellipses.
It’s too bad that you didn’t explain what you were really trying to do in the first place. It would’ve saved quite a bit of time. Since what you want is an elliptical arc between two points with given tangents, I think that the most straightforward way to go is simply to map a parameterized quarter-circle to the destination points. Since affine transformations preserve tangents, this will give you an elliptical arc with the correct tangents that’s relatively simple to trace: the quarter circle is $\mathbf p'(t)=(1-\sin t,1-\cos t)$, which makes the arc $$x=x_0+(x_1-x_0)(1-\sin t)+(x_2-x_0)(1-\cos t) \\ y=y_0+(y_1-y_0)(1-\sin t)+(y_2-y_0)(1-\cos t).$$ As $t$ goes from $0$ to $\pi/2$, the arc is traced from $(x_1,y_1)$ to $(x_2,y_2)$.
If the curve doesn’t necessarily have to be elliptical, consider using a quadratic Bézier curve instead. This will be a parabolic arc with the same tangents and end points, but the curve is much easier to trace. With the same three points as above, the curve is $(1-t)^2\mathbf p_1+2t(1-t)\mathbf p_0+t^2\mathbf p_2$, $0\le t\le1$. There are well-known methods for drawing such curves that you can easily find on the Internet.
For the example in your answer, $\mathbf p_0\approx(14.7567,6.)$, making the elliptical arc $$x \approx 10.2343 - 1.23429 \cos t + 5.76571 \sin t \\ y= 13. - 7. \cos t,$$ which is illustrated below.
For comparison, the broken blue line is the ellipse obtained by the original method with $s=3$ and the broken red line is the quadratic Bézier curve with those control points.
