Forgive me if this question has been asked before, but I did a quick search and nothing came up. My book (Geometry and Topology by Bredon) Defines components of a topological space $X$ as
The collection of equivalence classes of the equivalence relation "$p$ and $q$ belong to a connected subset of $X$"
while it defines quasicomponents as
The collection of equivalence classes of the equivalence relation "$d(p)=d(q)$ for every discrete valued map $d$ on $X$"
While I understand these definitions, I do have one misunderstanding: I don't understand how these concepts are different. The theorem
A topological space is connected iff every discrete valued map is constant
seems to show that they are one and the same:
Let $[\,\cdot\,]_C$ be the equivalence classes defined in the former definition and let $[\,\cdot\,]_Q$ be the equivalence classes defined in the latter definition.
$(\Rightarrow)$ (this direction is apparently true) If $[x]_C$ is the component in $X$ with $x$ as its representative, then for any $y\in [x]_C$, $x,y$ both belong to a connected subset of $X$. By the above we must then have $d(x)=d(y)$ for all discrete valued maps $d$. Thus $y\in [x]_Q$ and $[x]_C\subseteq [x]_Q$.
$(\Leftarrow)$ If $z,w\in [x]_Q$ are chosen arbitrarily, then $d(z)=d(x)$ and $d(w)=d(x)$ for all discrete valued maps $d$. But then $d(z)=d(w)$ for all discrete valued maps, so the above shows that $[x]_Q$ is connected, and hence $[x]_Q\subseteq [x]_C$.
The $(\Leftarrow)$ direction is evidently wrong. But why? A few months ago I encountered this same issue and apparently overcame it, but I forgot how. Thanks in advance.
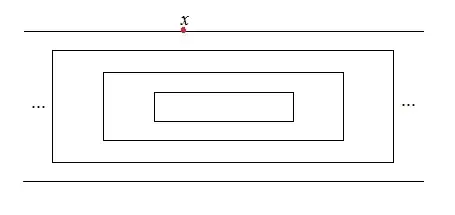
My "proof" doesn't work for your (wonderfully illustrative) example because, while all discrete valued maps on the whole space are constant on the two horizontal lines, we can still find a discrete valued map defined only on the two horizontal lines which is not constant. This shows disconnectedness. Tricky.
Thanks for all of your help. This is not the first time you've helped me either!
– Blake Aug 06 '16 at 21:43