Let $f$ be a differentiable real function. In many situations a solution of $f(x)=x$ can be found as limit of the recurrent sequence determined by some initial value and the recurrence $x_{n+1}=f(x_n)$.
To list only a few examples:
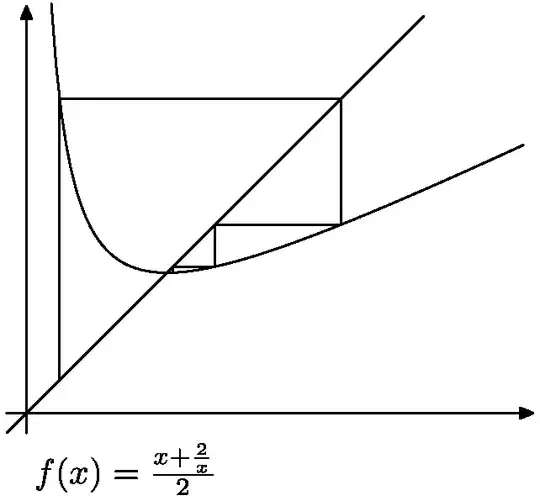
- For $f(x)=\frac{x+\frac ax}x$ where $a>0$ we get Babylonian methods for calculating square roots, see Proof of Convergence: Babylonian Method $x_{n+1}=\frac{1}{2}(x_n + \frac{a}{x_n})$
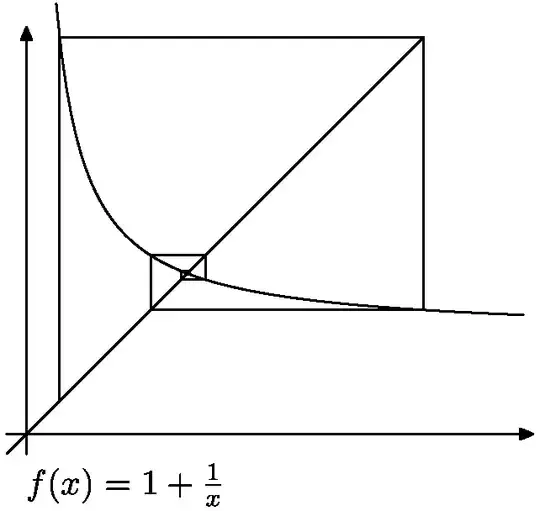
- Using $f(x)=1+\frac1x$ we get golden ratio as the limit. This corresponds to the continued fraction expansion of golden ratio and the convergence of the convergents.
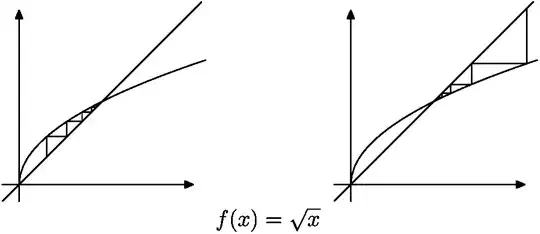
- For $f(x)=\sqrt x$ the recurrent sequence converges to $1$.
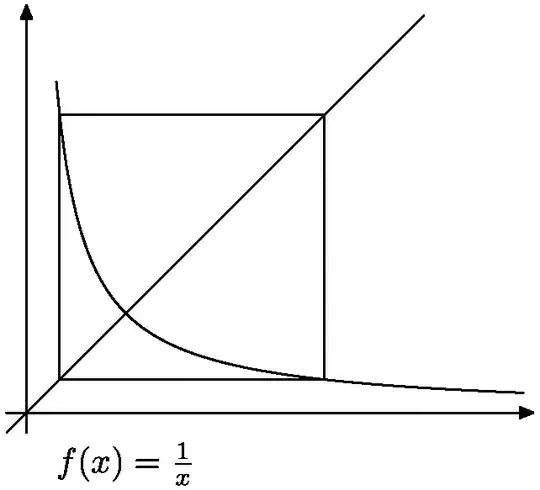
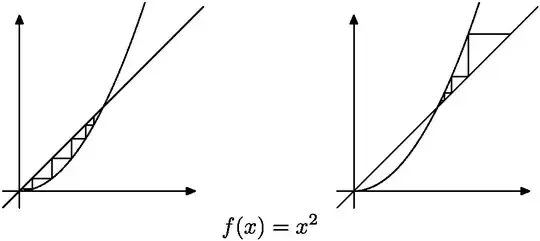
Of course, it can happen that the iterations do not converge. Examples of such functions are $1/x$ and $x^2$.
Fixed point iterations can be illustrated nicely with cobweb plots. The plots corresponding to functions I mentioned above are shown below. More similar illustration can be found here or elsewhere.
From the pictures it seems that the local behavior of $f'(x)$ might be enough to describe the behavior of the iterated sequence. (Whether it converges or not, whether the convergence is monotone, etc.) At least in the case that $|f'(x)|\ne1$ in some interval around the solution.
- What can be said about the sequence given by $x_{n+1}=f(x_n)$ if we have information about the values of $f'(x)$ close to the fixed point of $f$?
- Are there some references with proofs, related results, and so on.?
Illustration of Babylonian method for $f(x)=\frac12(x+\frac2x)$.
Illustration for iterations of $f(x)=1+\frac1x$
Iterations of $f(x)=\sqrt x$
Iterations of $f(x)=\frac1x$
Iterations of $f(x)=x^2$