I'm following a solution from here (the first problem), I don't understand how to "project $x_2$ onto $u_1$"
1) how does:$\begin{bmatrix}0\\\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{bmatrix}$ turn into $\begin{bmatrix}0\\2\\2\end{bmatrix}$?
2) how does: $x_1 - proj = \begin{bmatrix}1\\2\\-2\end{bmatrix}$ ?? Shouldn't it be $\begin{bmatrix}0\\-1\\-1\end{bmatrix}$??
I suppose the answer you'd benefit from here is a description of how the Gram-Schmidt process works.
To understand that we need to understand orthogonal projection. First we consider the orthogonal projection of a vector $\vec v$ onto the one-dimensional subspace $\operatorname{span}(\vec u)$. It is defined to be the unique component -- denoted $\vec v_\|$ or $\operatorname{proj}_{\vec u}(\vec v)$ -- of $\vec v$ parallel to $\vec u$ such that $$\vec v = \vec v_\| + \vec v_\bot,\quad \vec v_\bot \cdot \vec u = 0$$
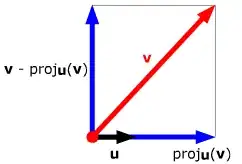
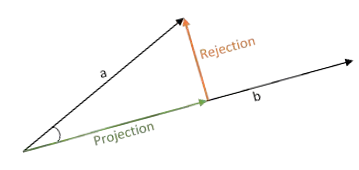
Before I give the formula, I'll give a geometric definition of the dot product that should make it much easier to understand where the formula comes from: the dot product $\vec v \cdot \vec u$ is the signed length of the projection of $\vec v$ onto $\operatorname{span}(\vec u)$ times the length of $\vec u$ where the sign is determined by the equation $\operatorname{proj}_{\vec u}(\vec v) = \lambda \vec u$ -- if $\lambda >0$, then the sign is $+$, otherwise it is $-$. For slightly more on this you can see this answer.
Then it should be easy to convince yourself that $$\operatorname{proj}_{\vec u}(\vec v) = \frac{\vec v\cdot \vec u}{\|\vec u\|^2}\vec u$$
(Note: don't take this as the definition of $\operatorname{proj}_{\vec u}(\vec v)$ or else we just get a circular set of definitions. The definition is in the first paragraph of this section -- this is just a formula for how to calculate $\operatorname{proj}_{\vec u}(\vec v)$)
But we don't only want to project a vector onto a one-dimensional subspace -- often we want to project a vector onto an arbitrary-dimensional subspace $U$.
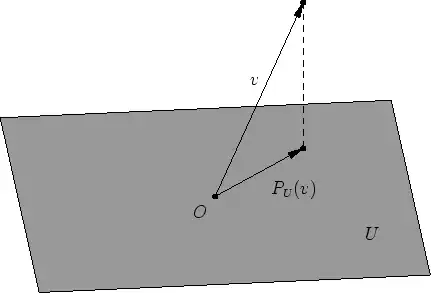
Once we have the one-dimensional orthogonal projection down, it's not too hard to extend it. Say we have an orthonormal basis $\{\vec u_1, \dots, \vec u_k\}$ for the subspace $U$. Then the orthogonal projection of $\vec v$ onto $U$ will simply be the sum of the projections onto each $\operatorname{proj}_{\vec u_i}(\vec v)$:
$$\operatorname{proj}_{U}(\vec v) = \sum_{i=1}^k \operatorname{proj}_{\vec u_i}(\vec v) = \sum_{i=1}^k \frac{\vec v\cdot \vec u_i}{\|\vec u_i\|^2}\vec u_i$$
Now ask yourself: why is this formula correct? Does the basis $\{\vec u_i\}$ really need to be orthonormal? (Hint for the second one: the answer is not quite, we can relax that restriction a little. Why?)
Now we have all the tools we need to describe the Gram-Schmidt process.
Let's say we have a basis $\{\vec b_1, \dots, \vec b_k\}$ of some $k$-dimensional subspace. That's great, but sometimes what we really want is an orthonormal basis. So that begs the question "is there some way of turning an arbitrary basis $\{\vec b_i\}$ into an orthonormal basis {\hat e_i}$?" The answer is yes. Here's the procedure:
First we're going to create an intermediate basis $\{\vec f_i\}$ which is orthogonal, but not necessarily orthonormal. We do so via a recurrence relation:
$$\begin{align}\vec f_1 &:= \vec b_1 \\ \vec f_i &:= \vec b_i - \operatorname{proj}_{U_{i-1}}(\vec b_i),\quad \text{for }1\lt i\le k\end{align}$$
where $U_{i-1} = \operatorname{span}(f_1, \dots, f_{i-1})$.
So what's happening here? Well first we just take the vector $\vec b_1$ and set $\vec f_1$ equal to it. Then for $\vec f_2$ we take $\vec b_2$ and subtract its projection onto $\vec f_1$. So what's left is just the component of $\vec b_2$ which is orthogonal to $\vec f_1$. Then for $\vec f_3$ we take $\vec b_3$ and subtract off its projection onto $\vec f_1$ and $\vec f_2$ to get just the part orthogonal to both. We continue in this way until we have an orthogonal basis $\{\vec f_i\}$.
But we didn't just want an orthogonal set, we wanted an orthonormal set. But now the normalization part is easy. We just set $\hat e_i := \frac{\vec f_i}{\|\vec f_i\|}$ for all $i$.
Then we're done. We've created an orthonormal basis $\{\hat e_i\}$ from an arbitrary basis $\{\vec b_i\}$ which necessarily describes the same subspace. Success!
