1

I understand that for each of the $N$ eigenvalues (regardless of repeated or not) of an $N\times N$ symmetric matrix, the algebraic multiplicity and geometric multiplicity are equal. This means if an eigenvalue is repeated $M$ times, then we have exactly $M$ orthogonal eigenvectors associated with this eigenvalue.

What I haven't figured out are:

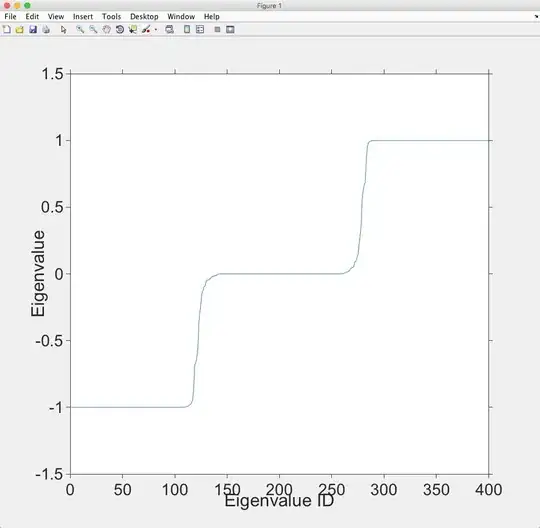
  1. Each entry of my $400\times400$ symmetric matrix is from $0$ to $1$ (both inclusive). I notice that many eigenvalues crowd at $0$, $-1$ and $1$, if they are not actually equal. On the other hand, eigenvalues elsewhere are well dispersed (figure below). Does this tell me anything about my symmetric matrix?

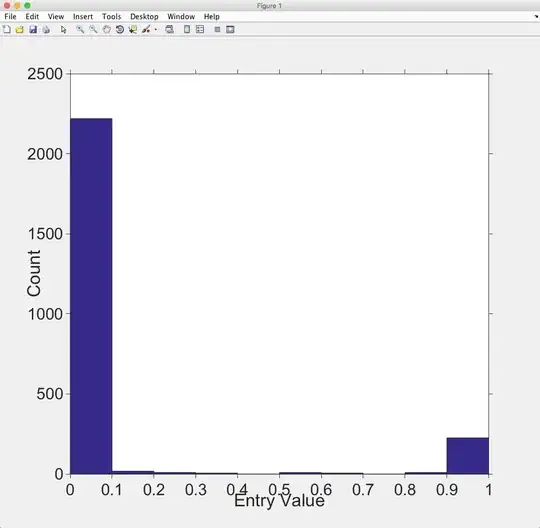
enter image description here

  1. In fact, entries of my matrix distribute weirdly between $0$ and $1$ in the sense that the predominant majority of the values (after I exlude zero entries) distribute between $0$ and $0.1$ (figure below). Maybe this has something to do with the result above?

enter image description here

  1. If this is not a numerical issue (i.e., the eigenvalues are really repeated), when does a symmetric matrix have repeated eigenvalues? Or what can we say about such a matrix?
Sibbs Gambling
  • 415
  • Have a look at this – Jean Marie Jul 25 '16 at 05:03
  • @JeanMarie Thanks for the article, which seems to suggest it's unsurprising to get a lot of eigenvalues centered around $0$. But I think the reason why so many eigenvalues clustered towards the two extremes seems still unclear. Thanks again! – Sibbs Gambling Jul 25 '16 at 08:34
  • You are right, Wigner's semicircle law (http://mathworld.wolfram.com/WignersSemicircleLaw.html) mentioned in the article does not account for your very "peaky" distribution (three peaks in $-1,0$ and $1$). Could it be that you have a bias in the generation of your symmetric matrices, which would not be as general as you think ? Could you provide your code ? – Jean Marie Jul 25 '16 at 12:12

0 Answers0