Not understanding derivative of a matrix-matrix product.

Question

I am trying to figure out a the derivative of a matrix-matrix multiplication, but to no avail. This document seems to show me the answer, but I am having a hard time parsing it and understanding it.

Here is my problem: We have $\mathbf{D} \in \Re^{m n}$, $\mathbf{W} \in \Re^{m q}$, and $\mathbf{X} \in \Re^{q n}$. Furthermore, $\mathbf{D} = \mathbf{W}\mathbf{X}$. (NOT an element wise multiplication - a normal matrix-matrix multiply).

I am trying to derive the derivative of $\mathbf{D}$, w.r.t $\mathbf{W}$, and the derivative of $\mathbf{D}$, w.r.t $\mathbf{X}$.

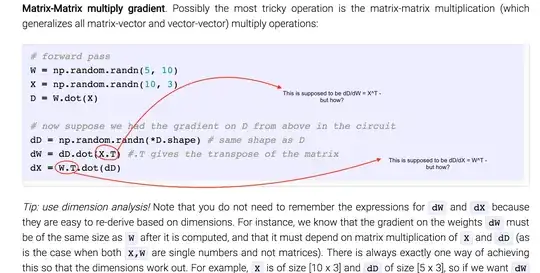
My class note this is taken from seems to indicate that $$ \frac{\delta \mathbf{D}}{\delta \mathbf{W}} = \mathbf{X}^{T} \text{ and that } \frac{\delta \mathbf{D}}{\delta \mathbf{X}} = \mathbf{W}^{T}, $$ but I am floored as to how he derived this. Furthermore, in taking the derivatives, we are asking ourselves how every element in $\mathbf{D}$ changes with perturbations by every element in, say, $\mathbf{X}$, - so wouldn't the resulting combinations blow up to be a-lot more than what $\mathbf{W}^{T}$ has? I cant even see how the dimensionality is right here.

EDIT: Id like to add the context of this question. It's coming from here, and here is my marked screen-shot of my problem. How are they deriving those terms? (Note: I understand the chain-rule aspect, and I am not wondering about that. I am asking about the simpler intermediate step).

Thanks.

Answer 1

For the first question alone (without context) I'm going to prove something else first (then check the $\boxed{\textbf{EDIT}}$ for what is asked):

Suppose we have three matrices $A,X,B$ that are $n\times p$, $p\times r$, and $r\times m$ respectively. Any element $w_{ij}$ of their product $W=AXB$ is expressed by:

$$w_{ij}=\sum_{h=1}^r\sum_{t=1}^pa_{it}x_{th}b_{hj}$$ Then we can show that: $$s=\frac {\partial w_{ij}}{\partial x_{dc}}=a_{id}b_{cj}$$ (because all terms, expect the one multiplied by $x_{dc}$, vanish)

One might deduce (in an almost straightforward way) that the matrix $S$ is the Kronecker product of $B^T$ and $A$ so that:$$\frac {\partial AXB}{\partial X}=B^T⊗A$$

Replacing either $A$ or $B$ with the appropriate identity matrix, gives you the derivative you want.

$$\boxed{\textbf{EDIT}}$$

Upon reading the article you added (and after some sleep!), I've noticed that $dD$ is not $\partial D$ in their notation, but rather $\dfrac {\partial f}{\partial D}$ where $f$ is a certain function of $W$ and $X$ while $D=WX$. This means that the first expression you're having problems with is $$\frac{\partial f}{\partial W}=\frac{\partial f}{\partial D}X^T$$ Since the author at the beginning stated that he'd use the incorrect expression "gradient on" something to mean "partial derivative" with respect to that same thing. So any element of $\partial f/\partial W$ can be written as $\partial f/\partial W_{ij}$. And any element of $D$: $$D_{ij}=\sum_{k=1}^qW_{ik}X_{kj}$$

We can write $$df=\sum_i\sum_j \frac{\partial f}{\partial D_{ij}}dD_{ij}$$ $$\frac{\partial f}{\partial W_{dc}}=\sum_{i,j} \frac{\partial f}{\partial D_{ij}}\frac{\partial D_{ij}}{\partial W_{dc}}=\sum_j \frac{\partial f}{\partial D_{dj}}\frac{\partial D_{dj}}{\partial W_{dc}}$$ This last equality is true since all terms with $i\neq d$ drop off. Due to the product $D=WX$, we have $$\frac{\partial D_{dj}}{\partial W_{dc}}=X_{cj}$$ and so $$\frac{\partial f}{\partial W_{dc}}=\sum_j \frac{\partial f}{\partial D_{dj}}X_{cj}$$ $$\frac{\partial f}{\partial W_{dc}}=\sum_j \frac{\partial f}{\partial D_{dj}}X_{jc}^T$$

This means that the matrix $\partial f/\partial W$ is the product of $\partial f/\partial D$ and $X^T$. I believe this is what you're trying to grasp, and what's asked of you in the last paragraph of the screenshot. Also, as the next paragraph after the screenshot hints, you could've started out with small matrices to work this out before noticing the pattern, and generalizing as I attempted to do directly in the above proof. The same reasoning proves the second expression as well...

Answer 2

Like most articles on Machine Learning / Neural Networks, the linked document is an awful mixture of code snippets and poor mathematical notation.

If you read the comments preceding the code snippet, you'll discover that dX does not refer to an increment or differential of $X,$ or to the matrix-by-matrix derivative $\frac{\partial W}{\partial X}.\;$ Instead it is supposed to represent $\frac{\partial \phi}{\partial X}$, i.e. the gradient of an unspecified objective function $\Big({\rm i.e.}\;\phi(D)\Big)$ with respect to one of the factors of the matrix argument: $\;D=WX$.

Likewise, dD does not refer to an increment (or differential) of D but to the gradient $\frac{\partial \phi}{\partial D}$

Here is a short derivation of the mathematical content of the code snippet. $$\eqalign{ D &= WX \\ dD &= dW\,X + W\,dX \quad&\big({\rm differential\,of\,}D\big) \\ \frac{\partial\phi}{\partial D} &= G \quad&\big({\rm gradient\,wrt\,}D\big) \\ d\phi &= G:dD \quad&\big({\rm differential\,of\,}\phi\big) \\ &= G:dW\,X \;+ G:W\,dX \\ &= GX^T\!:dW + W^TG:dX \\ \frac{\partial\phi}{\partial W} &= GX^T \quad&\big({\rm gradient\,wrt\,}W\big) \\ \frac{\partial\phi}{\partial X} &= W^TG \quad&\big({\rm gradient\,wrt\,}X\big) \\ }$$ Unfortunately, the author decided to use the following variable names in the code:

• dD   for $\;\frac{\partial\phi}{\partial D}$
• dX   for $\;\frac{\partial\phi}{\partial X}$
• dW   for $\;\frac{\partial\phi}{\partial W}$

With this in mind, it is possible to make sense of the code snippet $$\eqalign{ {\bf dW} &= {\bf dD}\cdot{\bf X}^T \\ {\bf dX} &= {\bf W}^T\cdot{\bf dD} \\ }$$ but the notation is extremely confusing for anyone who is mathematically inclined.
(NB: This answer simply reiterates points made in GeorgSaliba's excellent post)

Answer 3

Just to add to GeorgSaliba's excellent answer, you can see this must be the case intuitively.

Given a function $f(D)$ with $D=WX$, if all variables were scalars, we clearly have $$\frac{\partial f}{\partial W}=\frac{\partial f}{\partial D}\frac{\partial D}{\partial W}=\frac{\partial f}{\partial D}X$$ Now in the non-scalar case we expect the same exact form, up to some change of multiplication order, transpose, etc., due the non-scalar nature, but the overall form has to reduce to the same form in the scalar case, so it can't really be substantially different from the above.

Now, ${\partial f}/{\partial \bf D}$ in the non-scalar case has the same dimensions of $\bf D$, say a $n \times p$ matrix, but $\bf X$ is an $m × p$ matrix, which means we can't really do the multiplication as it stands. What we can do, is transpose $\bf X$, allowing us to do the multiplication, and giving the correct result of $n \times m$ for ${\partial f}/{\partial \bf W}$ which of course must have the same dimensions as $\bf W$. Thus, we see that we must have: $$\frac{\partial f}{\partial \bf W}=\frac{\partial f}{\partial \bf D}{\bf X}^T$$ One can formalize this into an actual proof, but we'll let this stand as only an intuitive guide for now.

Answer 4

You note is not correct, you missed the trace function, i.e. $\frac{\partial tr(XA) }{\partial X} = A^T$, check the 'Derivative of traces' section of the Matrix Cookbook.

Having said that, the confusion here is that you are trying to take the derivative w.r.t. a matrix of a MATRIX-VALUED function, the result should be a four-way tensor (array). If you check the Matrix Cookbook, it always talks about SCALAR-VALUED function. So I guess you missed some function here around D, maybe det() or trace(). Otherwise, you have to take derivative of each element of D, which will give you a matrix for each element.

Answer 5

I think your note is not correct.

$$f_{ij}=w_{ik}x_{kj}$$

$$\frac{\partial {f_{ij}}}{\partial {w_{mn}}}=tr(M)$$ where M is a block matrix and its diagonal is $X^T$ and its other element matrix is null matrix.

Answer 6

Not an answer, just the code from cs231n + print statements to see "small, explicit examples", here 0 / 1:

#!/usr/bin/env python
# -*- coding: utf-8 -*-

# https://math.stackexchange.com/questions/1866757/not-understanding-derivative-of-a-matrix-matrix-producto
# http://cs231n.github.io/optimization-2/#mat  Gradients for vectorized operations
# Work with small, explicit examples  here 0 / 1

from __future__ import division, print_function
import numpy as np

def pname( name ):
    """ pname( "name" / "expr" ): eval -> num / vec / array, print """
    A = eval(name)
    print( "\n%s %s: \n%s" % (
            name, getattr( A, "shape", "" ), A ))

np.random.seed( 3 )  # reproducible randint
W = np.random.randint( 0, 2, size=(5, 10) )  # [0, 2): 0 / 1
X = np.random.randint( 0, 2, size=(10, 3) )

Y = W.dot(X)  # D in the original
# now suppose we had the gradient on Y  -- here means ∂f/∂Y, for some f( Y )
dY = np.random.randint( 0, 2, size=Y.shape )
dW = dY.dot(X.T)
dX = W.T.dot(dY)

print( """
--------------------------------------------------------------------------------
Y = W.dot(X)
dY = ∂f/∂Y, for some f( Y )
dW = ∂f/∂W = ∂f/∂Y ∂Y/∂W = ∂f/∂Y . Xᵀ
dX = ∂f/∂X = ∂f/∂Y ∂Y/∂X = Wᵀ . ∂f/∂Y
--------------------------------------------------------------------------------
""" )

for name in "W X Y dY dW dX ".split():
    pname( name )