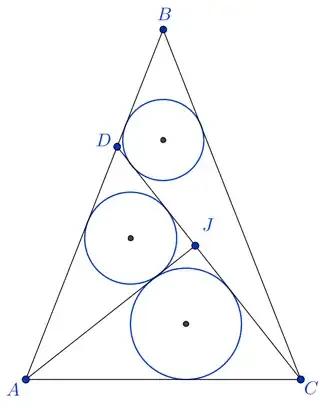
In $\triangle ABC$, $AB = BC$. If one chooses $D$ on $AB$ and $J$ on $CD$ such that $AJ \bot CD$ and the incircles of $\triangle ACJ$, $\triangle ADJ$, and $\triangle BCD$ all have radius $r$, then $r = AJ/4$.
How to prove it?
It is easy to notice that $r_{AJD}=r_{AJC}$ implies that $J$ is the midpoint of $CD$, since $AJD$ and $AJC$ are right triangles sharing a leg. How that relates to $r_{BCD}$?
You already proved $AC=AD$, hence we may assume that $AC=1$ and $\widehat{CAJ}=\theta$.
In such a way, $\widehat{DBC}=\frac{\pi}{2}-2\theta$ and $$ r = r_{CAJ} = \frac{2[CAJ]}{CA+AJ+JC} = \frac{\sin\theta\cos\theta}{1+\sin\theta+\cos\theta}.$$
Moreover, we have:
$$ CD=2\sin\theta,\quad AB=BC=\frac{1}{2\cos(2\theta)},\quad BD=\frac{1}{2\cos(2\theta)}-1. $$
If we write $2[CBD]$ and $CB+BD+DC$ in terms of $\theta$, the equation $r_{CAJ}=r_{CBD}$ boils down to $$\tan\theta=\frac{3}{4},$$
leading to $r=\frac{1}{5}$ and $AJ=\cos\theta=\frac{4}{5}$, from which $\color{red}{AJ=4r}$ as wanted.