The usual way trigonometric ratios are geometrically defined is always relative to an acute angle. So this way inside a right triangle, the trigonometric ratios are defined by the ratios of hypotenuse, base, and perpendicular. But when it's about angles greater than $90^\circ$? How can the ratios be related to hypotenuse, base, and perpendicular when angles greater than $90^\circ$ don't exist in right triangles?
If an angle $\theta$ is between $\pi/2$ and $\pi$, use the "reference angle" $\alpha = \pi - \theta$, and the fact that $\sin(\alpha) = \sin(\theta)$ and $\cos(\alpha) = -\cos(\theta)$.
Similarly, if $\pi < \theta < 3\pi/2$, then use the reference angle $\alpha = \theta - \pi$, and the facts that $\sin(\alpha) = -\sin(\theta)$ and $\cos(\theta) = -\cos(\alpha)$.
You can do a similar thing for the fourth quadrant, where the cosine will the same as the reference angle, and the sine will be negative.
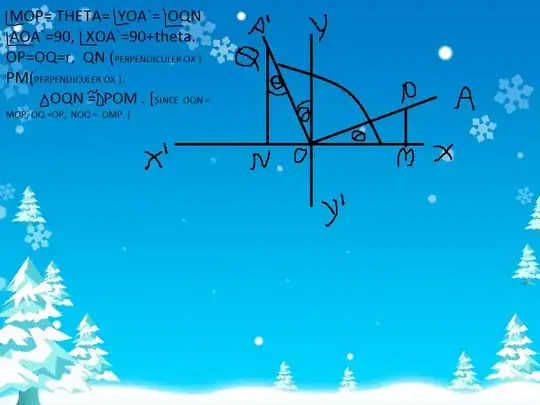
Think it like $sin\theta$ is projection of any vector on y-axis. $cos\theta$ projection on x-axis.
When you think about $sin\theta$, look at shadow of OQ on x-axis. projection of vector on y-axis will give you +ve y.
It tells $sin\theta$ is positive in 2nd quadrant.
When you think about $cos\theta$,look at shadow of OQ on x-axis. projection of vector on x-axis will give you -ve x.
It tells $cos\theta$ is negative in 2nd quadrant.
Similarly in 3rd and 4th quadrant.
