26

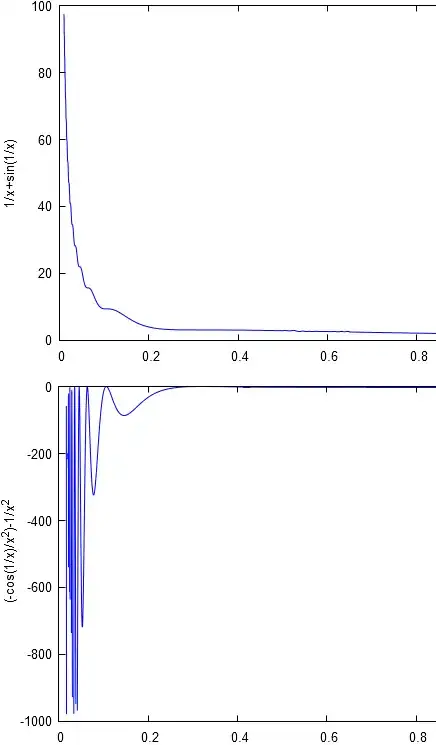
So here is what I understand:

  • If $f(x)$ is increasing/decreasing, then its derivative $f'(x)$ is positive/negative

and...

  • If $f(x)$ is increasing/decreasing, then the derivative of $f'(x)$ (which is $f''(x)$) is concave up/concave down

So my question is: if a graph has a vertical asymptote, the derivative must also have a vertical asymptote, too, right? Does it also work vice versa? I feel like there is a trick to it, but I'm not sure.

I have a graph from GeoGebra here. The dotted line is the derivative.

operatorerror
  • 29,103
miiworld2
  • 387
  • 4
    A side remark: you seem to assume $f$ is differentiable to being with (this may not be the case). Additionally, your comments on concavity seem off ($f$ monotone does not imply any concavity aspect for $f$ or $f'$. $f'$ monotone would imply concavity/convexity of $f$ -- is that what you mean?) – Clement C. Jul 18 '16 at 17:40
  • I agree the 2nd comment on concavity is off. It's been awhile since I had calculus, but I believe the statement should be, if $f(x)$ is concave up/down, then $f''(x)$ is positive/negative. – scott Jul 18 '16 at 21:04
  • both the statement used for monotone functions are wrong! The first one can be correct by making slight changes: if $f$ is differentiable and increasing (decreasing) on some interval then derivative $f'$ is non-negative (non-positive) on that interval. – Paramanand Singh Jul 19 '16 at 05:21

2 Answers2

50

if a graph has vertical asymptote, the derivative must also have a vertical asymptote too, right?

No. A counterexample: $$f(x)=\frac{1}{x}+\sin\left(\frac{1}{x}\right)$$ This function is monotone and has a vertical asymptote at $x=0$. But its derivative has no limit.

enter image description here

leonbloy
  • 63,430
18

Not quite. Suppose $y = f(x)$ has a vertical asymptote at $x=a$ in the sense that $\lim_{x \to a\pm} f(x) = +\infty$ or $-\infty$. Then $\lim_{x \to a\pm} f'(x)$ can't be a finite number. It could be $+\infty$ or $-\infty$, but it also might not exist at all. In fact, $f'$ might not exist at all.

In the other direction, $f'$ can have a vertical asymptote without $f$ having one. For example, consider $f(x) = x^{2/3}$, $f'(x) = \dfrac{2}{3} x^{-1/3}$, with $a=0$.

Robert Israel
  • 448,999
  • 5
    As a contrived example I could think of: $f$ defined for $x>0$ by $f(x) = \int_1^x \frac{\sin^{2}\frac{1}{t}}{t} dt$ would do the job. ($f$ is differentiable and has a vertical asymptote at $0$, with $f'(x) = \frac{\sin^{2}\frac{1}{x}}{x}$ for $x>0$ — this has no limit, neither finite nor infinite, at $0$). – Clement C. Jul 18 '16 at 17:36
  • Thank you guys for all the explanation. – miiworld2 Jul 18 '16 at 18:59