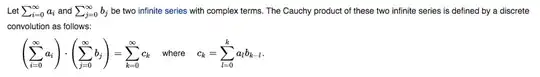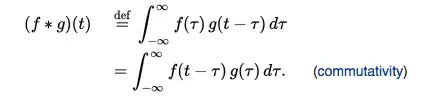5

I have been trying to do some problems in probability that use convolutions but there has not been much of an explanation of what a convolution is or the purpose of using a convolution.

For example in the following problem:

Let X and Y be two independent exponential distributions with mean $1$.

Find the distribution of $\frac{X}{Y}$.

So I define $U=\frac{X}{Y}$ and $V=Y$ then $$f_U(u)=\int_{-\infty}^{\infty}f_{XY}(uv,v)dv=\int_{0}^{\infty}e^{-uv}e^{-v}dv=\frac{1}{u+1}$$

Maybe one could explain a simpler problem:

Let X and Y be two random variables with joint density function $f_{XY}$ . Compute the pdf of $U = Y − X$. So I tried the following and maybe its correct I dont know just using formulas $$f_U(u)=\int_{-\infty}^{\infty}f_{XY}(x,u+x)dx=\int_{-\infty}^{\infty}f_{XY}(y-u,y)dy$$

I was given the formula $(f*g)(z)=\int_{-\infty}^{\infty}f(z-y)g(y)dy=\int_{-\infty}^{\infty}f(x)g(z-x)dx$

I do not fully understand what I am supposed to be putting into $f(z-y)g(y)$ part of the integrals specifically for $(z-y)$.

Community
  • 1
Andrew
  • 556
  • I think the main identity you are working with is that if $X,Y$ are independent random variables with pdfs $f,g$ respectively, then the pdf of $X+Y$ is $h(z)=(f*g)(z)$. Thus in your formulas $z$ is the argument to the pdf of $X+Y$ and $y$ is the integration variable. So your answer should depend on $z$ but not on $y$. This formula does not immediately apply to the problem of finding the distribution of $Y-X$. You can deal with this by rewriting the problem as $Y+(-X)$, and using the pdf of $-X$ (which in general is not the same as the pdf of $X$) in the formula above. – Ian Jul 18 '16 at 11:42
  • The expression for the first PDF of $U$, when $U=X/Y$ with $(X,Y)$ i.i.d. exponential, is wrong. – Did Jul 18 '16 at 17:21

1 Answers1

7

I will try to start from the simplest case possible and then build up to your situation, in order to hopefully develop some intuition for the notion of convolution.

Convolution essentially generalizes the process of calculating the coefficients of the product of two polynomials.

See for example here: Multiplying polynomial coefficients. This also comes up in the context of the Discrete Fourier Transform. If we have $C(x)=A(x)B(x)$, with $A(x), B(x)$ polynomials, we have: The image is from Cormen et al, Introduction to Algorithms, p. 899.

This type of operation also becomes necessary when calculating the probability distributions of discrete random variables. In fact, this type of formula allows us to prove that the sum of independent Bernoulli random variables is binomially distributed.

If we want to calculate the probability distribution of two discrete random variables with infinite support (for example, the Poisson distribution, which can take infinitely many possible values with positive probability), then we need to use the Cauchy product to calculate the convolution. This just generalizes the formula given above for infinite series. The following image is from Wikipedia:

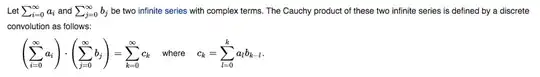
enter image description here

Now as you probably already know, the (Riemann) integral is the limit of infinite series, hence it should not be surprising that this convolution formula for infinite series also generalizes to a convolution formula for integrals. This is what you are working with for probability distributions of continuous random variables, as in your problem above.

Here is the formula (from Wikipedia again):

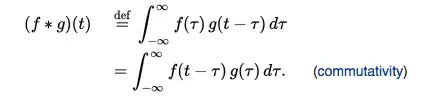
enter image description here

$U=Y-X = Y + (-X)$, so therefore $$f_U(u) =(f_Y * f_{-X})(u) = \int_{-\infty}^{\infty} f_Y(t) f_{-X}(u-t) \mathrm{d}t$$

Right now you only have the joint density, so in order to use the convolution formula, we have to calculate the marginal densities from the joint density. This will lead to us having a double integral. See for example here: How do I find the marginal probability density function of 2 continuous random variables? or Help understanding convolutions for probability?

More specifically (see e.g. here), $$f_Y(y) = \int_{-\infty}^{\infty}f_{XY}(x,y)dx$$ $$f_X(x) = \int_{-\infty}^{\infty} f_{XY}(x,y) dy$$ So now we have the (marginal) densities for $X$ and $Y$, but what we need are the densities for $-X$ and $Y$, so we need to calculate the density of $-X$ based on the density for $X$, which is done as follows (for $X$ continuous such that $\mathbb{P}(X=c)=0$ for any $c \in \mathbb{R}$): $$\mathbb{P}(a \le X < b)= \mathbb{P}(-b < X \le -a) \\ \implies \mathbb{P}(a \le -X < b) = \int_{-b}^{-a} f_X(x)dx = \int_b^a [f_X(-x)](-1) \mathrm{d}x=\int_a^b f_X(-x) \mathrm{d}x$$

In other words, $$f_{-X}(x)=f_X(-x) = \int_{-\infty}^{\infty} f(-x,y)\mathrm{d}y.$$

So finally, $$f_U(u)= \int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f_{XY}(x,t)\mathrm{d}x\right] \left[\int_{-\infty}^{\infty} f_{XY}(-(u-t),y)\mathrm{d}y \right]\mathrm{d}t = \int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f_{XY}(x,u-t)\mathrm{d}x \right] \left[ \int_{-\infty}^{\infty} f_{XY}(-t,y)\mathrm{d}y \right]\mathrm{d}t$$ The second version might be easier to calculate; both are equivalent.

Community
  • 1
Chill2Macht
  • 20,920
  • 4
    Thanks for this explanation it really helps. It seems to me that if we do not have $X$ and $Y$ independent we cannot perform a convolution so we perform a change of variables. – Andrew Jul 19 '16 at 00:54
  • 2
    Exactly the convolution formula does not hold for arbitrary $X$ and $Y$, but it does hold for independent $X$ and $Y$. (There might be non-independent $X$ and $Y$ for which it "accidentally" holds, which is why I didn't say that it only holds for independent $X$ and $Y$, but in practice one almost never runs into that phenomenon, and even if one did, it still would not affect the pertinent fact [$X$ and $Y$ independent] $\implies$ [convolution formula holds]) – Chill2Macht Jul 19 '16 at 00:57