circle tangent to three circles

Question

To-day I want to look at CCC - one circle tangent to three circles whose radii and positions of their centers are known.

How does one solve this.. old fashioned ways like ruler and compass, or modern ways like intersection theory?

these Apollonius problems are all very classical but good treatments are hard to find. here is a different such problem

construct circle tangent to two given circles and a straight line

Answer 1

Here is an outline of the a procedure. Assume first that you want to find a circle that encloses all three others and touches them from the outside.

1. Observe that if you increase the radii of all the three circles by the same amount, then the center of the surrounding circle will stay at the same point. Only its radius will increase (by the same amount). Therefore without loss of generality we can assume that two of the three circles intersect at a point $A$. After all we can achieve this by adjusting their radii.
2. Invert the whole picture w.r.t. a circle with center $A$ (pick one, doesn't matter which one you use). Remember that inversion preserves tangency, and takes circles to circles (or to lines in an important special case!). Because two circles passed via $A$, those two circles become lines in the inversion. Now we have the task of finding a circle that is tangent to a given circle and to given two lines.
3. Reusing the idea of the first stage we then shrink the remaining circle to have radius zero, i.e. shrink it to a point. At the same time we shrink the radii of the two lines by parallel transporting them by the same amount. Again, in this process the center of the sought after circle does not move.
4. We now face the problem of finding a circle that is tangent to two given lines and passes through a given point. Solving this is easy. Draw any circle tangent to the two lines (its center will be on the bisector of the angle formed by the two lines et cetera). That circle probably won't go through the point, but a simple application of homothety will fix that.
5. Undo steps 3,2 and 1 in that order. Inversion is its own inverse, and the other steps have the obvious inverse operations. Rejoice!

If you want to vary the way of tangency (inside/outside), then you may need to shrink some of the three circles instead of expanding their radii in step 1. Altogether there may be as many as eight solutions, for the fourth circle may be tangent to the other three in two ways. Some of those alternatives may not work. For example, if one of the three original circles is inside another, we get obvious problems. Also, should the three initial circles be concentric, there cannot be a solution, and in such a case already step 1 fails.

Answer 2

THIS IS A COMMENT NOT AN ANSWER.

In http://debart.pagesperso-orange.fr/seconde/contruc_cercle.html there are ten problems of contact concerning circles which are solved in a quite interesting way. The text is in French and the problem $10$ is the Apollonius’s consisting in finding a circle tangent to three given circles of which eight solutions are given.

Here a translation of the “Historique” of the subject. $$*****$$

“ The problem of the circle tangent to three circles is one of the great problems of history of geometry.

It was introduced by Pappus as the tenth and most difficult of the Treaty of contacts, one of the lost works of Apollonius.

In 1596, Adrien Romain (Van Roomen, Latinized as Adrianus Romanus, Flemish mathematician 1561-1615) propose a solution using a hyperbola, that Vieta considers not in accordance with the method of Ancients.

Indeed, the emergence of algebra in geometry allows him to claim that it is a problem of the second degree, so a plan problem which can be solve with "the ruler and compass."

Vieta published his own solution in 1600, in his Apollonius Gallus where he presents some lemmas for handling the similarities and where he exhibited the first nine situations listed above. It recognizes that the solutions to this problem tenth depend on the relative position of the three circles, but ignores the discussion of a lot of solutions and will have to wait until Descartes (1637) for discussion of particular solutions.

Until the nineteenth century, this problem will be one of the places of confrontation between the synthetic geometry (pure geometry) and analytical geometry."

Answer 3

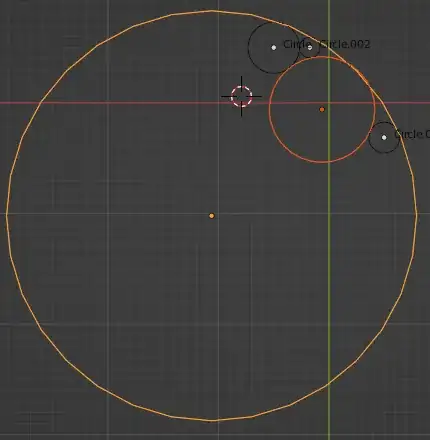
I was working on the same problem and got the solution:

1. we must obtain the system of equations of the 3 circles. The following is only for the first equation where x_1, y_1 and r_1 are the data of the known circle.

   (x - x_1)^2 + (y - y_1)^2 = r_1^2

2. The squares in the equation are expanded to simplify it.

3. Simplify the similar terms in the equation and set it equal to zero

4. The system of quadratic equations is solved.

As I mentioned, I was solving this same problem and programmed the solution in python:

from sympy import symbols, Eq, simplify
def devolverEcuacion(x1, y1, r1):
Definir la ecuación original
ecuacion_original = (x - x1)2 + (y - y1)2 - (r + r1)**2
Expandir los cuadrados
ecuacion_expandida = expand(ecuacion_original)
Simplificar términos semejantes
ecuacion_simplificada = collect(ecuacion_expandida, [x, y, r])
  eq = Eq(ecuacion_simplificada, 0)
  print(eq)
  return eq
Datos del primer círculo
x1, y1, r1 = -5.0, 5.0, 2.3255488872528076
eq1 = devolverEcuacion(x1, y1, r1)
Datos del segundo círculo
x2, y2, r2 = 5.0, -3.1395609378814697, 1.3953293561935425
eq2 = devolverEcuacion(x2, y2, r2)
Datos del tercer círculo
x3, y3, r3 = -1.7442314624786377, 5.0, 0.9302195310592651
eq3 = devolverEcuacion(x3, y3, r3)
Resolver el sistema de ecuaciones numéricamente
sol = solve((eq1, eq2, eq3), (r, x, y), dict=True)
Imprimir la solución
print("Solución:")
print(sol)

for this example:

Eq(-1.0*r**2 - 4.65109777450562*r + 1.0*x**2 + 10.0*x + 1.0*y**2 - 10.0*y + 44.5918223729972, 0)
Eq(-1.0*r**2 - 2.79065871238708*r + 1.0*x**2 - 10.0*x + 1.0*y**2 + 6.27912187576294*y + 32.9098988704157, 0)
Eq(-r**2 - 1.86043906211853*r + 1.0*x**2 + 3.48846292495727*x + 1.0*y**2 - 10.0*y + 27.1770350187362, 0)
Solución:
[{r: -18.5438116854768, x: -10.6217988468949, y: -10.2127389354221}, {r: 4.77849716604361, x: -0.626523746806375, y: -0.598229701442041}]

The solution has two options, the inner circle and the outer circle.

Answer 4

Closed form solution (S. Bancroft)

This problem is equivalent to solving the GPS pseudorange equations. There exist closed form methods to solve this problem. I present here the method developped by Bancroft [1] in the 80s.

Denote as $\bf{a}_i$ the center of the given circles and $\rho_i$ their radius. Denote as $\bf{x}_u$ the center of the unknown circle and $\beta$ its radius. The tangency contraint is:

\begin{align} & \|\bf{a}_j - \bf{x}_u\|^2 = (\rho_j - \beta)^2, \\ \Leftrightarrow \qquad & \|\bf{a}_j - \bf{x}_u\|^2 - (\rho_j - \beta)^2 = 0. \tag{1} \end{align}

Introduce the matrix $\bf{L} = \text{diag}(1,1,-1)$. It induces a pseudo-scalar product and a pseudo-norm on $\mathbb{R}^{3}$ defined as: \begin{align} <{(\bf{x}, \beta)},{(\bf{x}', \beta')}>_{\bf{L}} &= \bf{x}^\intercal \bf{x}' - \beta \beta', & N_{\bf{L}}(\bf{p}) &= <{\bf{p}},{\bf{p}}>_{\bf{L}}. \end{align} This pseudo-scalar product is bilinear, symmetrical but it is not definite (nor positive). With these notations the tangency equations $(1)$ is simply $N_{\bf{L}}(\bf{p}_u - \bf{p}_j) = 0$ where $\bf{p}_j = \begin{pmatrix}\bf{a}_j^\intercal & \rho_i\end{pmatrix}^{\intercal}$ is known and $\bf{p}_u = \begin{pmatrix}\bf{x}_u^\intercal & \beta\end{pmatrix}^{\intercal}$ is unknown. . It develops as: \begin{align} &&N_{\bf{L}}(\bf{p}_u) + N_{\bf{L}}(\bf{p}_j) - 2 <{\bf{p}_u},{\bf{p}_j}>_{\bf{L}} = 0, \\ \Leftrightarrow &&\qquad <{\bf{p}_u},{\bf{p}_j}>_{\bf{L}} = N_{\bf{L}}(\bf{p}_u)/2 + N_{\bf{L}}(\bf{p}_j)/2.\tag{2} \end{align} Introduce the auxiliary unknown $\lambda = N_{\bf{L}}(\bf{p}_u)/2$. The equations $(2)$ can be stacked as: \begin{equation} \bf{S}\bf{L}\bf{p}_u = \lambda \bf{1} + \bf{f}, \end{equation} where $\bf{S} \in \mathbb{R}^{3 \times 3}$ is the (known) matrix whose $j$-th row is $\bf{p}_j^\intercal$, and $\bf{f} \in \mathbb{R}^3$ is the vector whose $j$-th entry is $N_{\bf{L}}(\bf{p}_j)/2$.

Multiply by the inverse of $\bf{S}$, since $\bf{L}^{-1} = \bf{L}$: \begin{equation} \bf{p}_u = \bf{L}\bf{S}^{-1}(\lambda \bf{1} + \bf{f}) = \lambda \bf{L}\bf{u} + \bf{L}\bf{v}, \tag{3} \end{equation} where $\bf{u} = \bf{S}^{-1}\bf{1}$ and $\bf{v} = \bf{S}^{-1}\bf{f}$ are known.

Finally, take the pseudo-norm in $(3)$ to get: \begin{equation}\label{eq: Bancroft polynome en lambda} \lambda^2 N_{\bf{L}}(\bf{u}) + 2\lambda (<{\bf{u}},{\bf{v}}>_{\bf{L}} - 1) + N_{\bf{L}}(\bf{v}) = 0, \tag{4} \end{equation} The position $\bf{p}_u$ is obtained by $(i)$ solving the polynomial equation $(4)$ for $\lambda$, then $(ii)$ reinjecting in $(3)$.

This method gives the two solutions of the problem. It can be extended to any dimension $d \ge 2$ by considering $d+1$ "circles".

---

[1] Bancroft, S. (1985). An algebraic solution of the GPS equations. IEEE transactions on Aerospace and Electronic Systems, (1), 56-59.