How can it be proved that the limit definition and series definition of $e$ are equivalent, how do they model continuous growth?

Question

The limit definition of $e$ gives the best intuition toward how $e$ can model continuous growth.

$$\lim\limits_{n \to \infty} \left( 1 + \frac1n\right)^n$$

Let n represent n moments of growth that scale the initial value by $ 1 + \frac1n $.

The key to me seems to be that the $\Delta x $ approaches 1 but does not reach it. This allows for the best approximation $\Delta x = 1 $ at each moment. In other words, at each moment of growth the value x experiences $\Delta x = 1 + \frac1n $, or as $n \to \infty$... $$\lim\limits_{n \to \infty} 1 + \frac1n = 1 $$

Growth with n = 2 moments:

$1 \times 1\frac12 \times 1\frac12 $ = 2.25

insight: If 2 moments of growth occur to x where $\Delta x = 1\frac12$, this amounts to discrete growth by $\Delta x = 1\frac12$ twice.

Growth with three moments:

$1\times 1\frac13 \times 1\frac13 \times 1\frac13 $ = 2.35

insight: If 3 moments of growth occur to x in where $\Delta x = 1\frac13$, this amounts to discrete growth by $\Delta x = 1\frac13$ three times.

Growth at seven moments:

$1\times \frac17 \times 1\frac17 \times 1\frac17 \times 1\frac17 \times 1\frac17 \times 1\frac17 \times 1\frac17 $ = 2.55

insight: If 7 moments of growth occur to x in this period where $\Delta x = 1\frac17$, this amounts to discrete growth by $\Delta x = 1\frac17$ seven times.

$\lim\limits_{n \to \infty} \left( 1 + \frac1n\right)^n $ is a definition of $e$ as it models n moments of growth occurring where at each instant the initial value is scaled by a factor $\lim\limits_{n \to \infty} 1 + \frac1n = 1 $.

To me this seems intuitive to a small extent. If we want to grow continuously we scale by an infinitely small increase an infinite number of times and this converges onto the number $e$. Why it must converge is mysterious to me, and besides seeing a proof I can't intuit to something that is satisfying.

Now there is also the Taylor series representation of $e$

$$ \sum_{n=0}^\infty \frac1{n!} = 1 + 1 + \frac12 + \frac1{3\times2\times1} + \frac1{4\times3\times2\times1} ... $$

Speaking loosely it seems to get $e$ you can sum a whole and itself, with $ \frac12$ that whole, and $ \frac13$ of $ \frac12$ of that whole and so on...and I have no intuition for this.

Again, the Taylor Series converges to $e$ but I don't see the same intuition for how this can model continuous growth. Furthermore, with my limited math skills I wouldn't know how to prove:

$$\lim\limits_{n \to \infty} \left( 1 + \frac1n\right)^n = \sum_{n=0}^\infty \frac1{n!}$$

My 3 questions I am seeking to answer are

1. By what application or intuition can it be seen that $ \sum_{n=0}^\infty \frac1{n!} $ models continuous growth?

2. What are some proofs that:

$$\lim\limits_{n \to \infty} \left( 1 + \frac1n\right)^n = \sum_{n=0}^\infty \frac1{n!}$$

3. Is euler's number inextricably linked to time as $\pi$ is to the circle?

When discussing $e$ it seems necessary to talk of periods of continuous growth $ p = kt $ being represented by $ e = e^p $ where $ p = 1 $ in the fundamental case. I do not know how to think of $e$ without seeing it as one period of continuous growth proven to be $e$ by the convergence of the intuitive definition I gave. I cannot see this same inextricable link to a period in the Taylor Series nor in other definitions of $e$.

Thanks for any comments, I have been trying to wrap my head around $e$ at the most fundamental level for a long time so that I can more deeply understand differential equations.

How was it arrived upon that e best modeled continuous growth? Was it an experimental observation or was it a proof that convinced mathematicians and scientists that $e$ embodies the idea of continuous growth i.e. growth at all instances?

I have so many questions about Taylor Series and $e^{i\theta}$ I'm trying to answer as well..

Best Wishes,

Answer 1

The following deals with your second question.

---

Without adding any additional details about $e$ and $\log$ here is the proof of the identity $$\lim_{n \to \infty}\left(1 + \frac{1}{n}\right)^{n} = \lim_{n \to \infty}\left(1 + \frac{1}{1!} + \frac{1}{2!} + \cdots + \frac{1}{n!}\right)$$ I assume that you are aware of the fact that both the limits above exist (it is easy to establish this by noting that both the sequences involved here are increasing and bounded above).

Let $$a_{n} = \left(1 + \frac{1}{n}\right)^{n}, b_{n} = 1 + \frac{1}{1!} + \frac{1}{2!} + \cdots + \frac{1}{n!}$$ and also consider another related sequence $$c_{n} = \left(1 - \frac{1}{n}\right)^{-n}$$ Clearly we have \begin{align} \lim_{n \to \infty}c_{n} &= \lim_{n \to \infty}\left(1 - \frac{1}{n}\right)^{-n}\notag\\ &= \lim_{n \to \infty}\left(\frac{n}{n - 1}\right)^{n}\notag\\ &= \lim_{n \to \infty}\left(1 + \frac{1}{n - 1}\right)^{n - 1}\cdot\frac{n}{n - 1}\notag\\ &= \lim_{n \to \infty}\left(1 + \frac{1}{n - 1}\right)^{n - 1}\notag\\ &= \lim_{n \to \infty}a_{n} \text{ (replacing }n - 1\text{ by } n)\notag \end{align} Using binomial theorem we can see that \begin{align} a_{n} &= \left(1 + \frac{1}{n}\right)^{n}\notag\\ &= 1 + 1 + \frac{n(n - 1)}{2!}\cdot\frac{1}{n^{2}} + \cdots\notag\\ &= 1 + 1 + \dfrac{1 - \dfrac{1}{n}}{2!} + \dfrac{\left(1 - \dfrac{1}{n}\right)\left(1 - \dfrac{2}{n}\right)}{3!} + \cdots\notag\\ &\leq 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \cdots + \frac{1}{n!}\notag\\ &= b_{n}\notag \end{align} Similarly if $n > 1$ then we can use the binomial theorem for general index to get \begin{align} c_{n} &= \left(1 - \frac{1}{n}\right)^{-n}\notag\\ &= 1 + 1 + \frac{n(n + 1)}{2!}\cdot\frac{1}{n^{2}} + \cdots\notag\\ &= 1 + 1 + \dfrac{1 + \dfrac{1}{n}}{2!} + \dfrac{\left(1 + \dfrac{1}{n}\right)\left(1 + \dfrac{2}{n}\right)}{3!} + \cdots\notag\\ &\geq 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \cdots + \frac{1}{n!}\notag\\ &= b_{n}\notag \end{align} It thus follows that if $n > 1$ then we have $$a_{n} \leq b_{n} \leq c_{n}$$ Both sequences $a_{n}, c_{n}$ tend to same limit hence by applying Squeeze theorem theorem it follows that $b_{n}$ also tends to the same limit and our job is done. The same technique can be used to prove the more general result that $$\lim_{n \to \infty}\left(1 + \frac{x}{n}\right)^{n} = \lim_{n \to \infty}\sum_{i = 0}^{n}\frac{x^{i}}{i!}$$ for all real numbers $x$.

Answer 2

There are some assumptions you have to make in what respect $e$ is introduced. My approach is that it is known that the derivative of $y=\ln x$ is equal to $y=1/x$. Now using the limit definition of the derivative, we have :

$$\lim\limits_{x \to 0} \frac{\ln(x+1)-\ln1}{x}=1$$ The $1$ on the right hand side is the derivative of $\ln x$ in which we substituted $1$. Since $\ln1=0$, we can do some algebra: Bring the $x$ in the denominator upfront as $\frac{1}{x}$ which then can be put as an exponent by laws of logs:

$$\lim\limits_{x \to 0} \ln(x+1)^\frac{1}{x}=1$$

Raising both sides to power $e$ we get: $$\lim\limits_{x \to 0} (x+1)^\frac{1}{x}=e$$ When you perform a substitution $x=1/n$, you get your limit "connected" to $e$. Hope this input addresses some of your questions. (essentially your introductory part)

Answer 3

You're asking multiple questions here, and you've asked them in a certain order. But I'm gonna take a liberty and answer them in a more intuitive order.

In your third question, you asked if Euler's number is inextricably linked to time. It is, in fact, not. Euler's number is inherently a mathematical constant, not a physical one. While it may be useful regarding time dependent functions, that doesn't necessarily mean that it is fundamentally tied to time dependent functions as $\pi$ is to circles.

You see, fundamentally the number $e$ is about $2$ things. Exponential growth, and rate of change. The first thing to consider is the derivative of any exponential. Let's begin by differentiating a random exponential $a^x$.

$$\frac{d(a^x)}{dx} = \lim_{h \to 0} \frac{a^{x+h} - a^x}{h}$$

As $a^{x+h} = a^x a^h$,

$$\frac{d(a^x)}{dx} = \lim_{h \to 0} \frac{a^x a^h - a^x}{h}$$

Factoring out $a^x$ from the numerator, and outside the limit gives us

$$\frac{d(a^x)}{dx} = a^x \lim_{h \to 0} \frac{a^h - 1}{h}$$

From this, we can intuitively see that the derivative of any exponential is going to be directly proportionate to the exponential itself, as the derivative of $a^x$ is equal to $a^x$ times some constant. The question then arises: does there exist a base for which this proportionality constant is equal to $1$? Is there a function such that the function is its own derivative?

The short answer to this is yes. And we have with us the means to find it. The first thing to do is to take $\lim_{h \to 0} \frac{a^h - 1}{h}$ to be our proportionality constant. But we also know that our proportionality constant must be $1$. Hence, we get

$$\lim_{h \to 0} \frac{a^h - 1}{h} = 1$$

multiplying $\lim\limits_{h \to 0} h$ on both sides, we get:

$$\lim_{h \to 0} \frac{a^h - 1}{h} \lim_{h \to 0} h = \lim_{h \to 0} h$$

Collecting the limits on the left hand side gives us

$$\lim_{h \to 0} \frac{a^h - 1}{h} h = \lim_{h \to 0} a^h - 1 = \lim_{h \to 0} h $$

bringing the $1$ on the left hand side to the right hand side gives us

$$\lim_{h \to 0} a^h = \lim_{h \to 0} h + 1$$

Some amount of finagling of the expression will hence give us

$$a = \lim_{h \to 0} (h + 1)^{\frac{1}{h}}$$

let us now state that $\frac{1}{h} = n$. This is equivalent to stating $\frac{1}{n}=h$. When $n\to\infty$, $h\to0$. Hence, we can now rewrite out original limit as being

$$a = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n$$

This is where the limit definition of Euler's number comes from. From this, we can know for certain a fundamental (if not the defining property of) the number $e$. And more importantly, it helps us understand why the derivative of $e^x$ is $e^x$. It isn't a coincidence, it's the very definition of $e$! If you're determined to find a connection between $e$ and some property as $\pi$ is to circles, then here it is: the holy grail. Euler's number is fundamentally and inextricably linked to rate of change problems. Although this is an idea you seem to have grasped intuitively, even before considering the underlying calculus.

Questions $1$ and $2$ can be answered simultaneously. By proving that the limit and series definitions of $e^x$ are equivalent, we can show definitively that there is a link between the Taylor series and exponentiation. The intuition will come naturally once you can see how the two can be equated directly without using the exponential function as an explicit intermediate.

This is slightly more difficult to prove (or rather, more difficult on my stubby little fingers as I do my best to work out the LaTex)

Let us begin by only considering the expression

$$\left(1+\frac{1}{n}\right)^n$$.

We can expand the brackets by using the binomial theorem as follows:

$$\left(1+\frac{1}{n}\right)^n = \sum_{k=1}^n \frac{n!}{k!(n-k)!n^k}$$

By doing some simplifications we get

$$\left(1+\frac{1}{n}\right)^n = 1 + \sum_{k=1}^n \frac{\prod\limits_{j=1}^{k-1} (n-j)}{k!n^{k-1}}$$

Simplification is a relative term. It comes together later though, I swear. Given $x\in\mathbb N$, we can state that

$$n^x = \prod_{i=1}^x n$$

We can hence use this information to state that

$$\left(1+\frac{1}{n}\right)^n = 1 + \sum_{k=1}^n \frac{1}{k!} \prod\limits_{j=1}^{k-1} \frac{(n-j)}{n}$$

This is equal to

$$1 + \sum_{k=1}^n \frac{1}{k!} \prod_{j=1}^{k-1} \left(1 - \frac{j}{n}\right)$$

Therefore, we can state that

$$\left(1+\frac{1}{n}\right)^n = 1 + \sum_{k=1}^n \frac{1}{k!} \prod_{j=1}^{k-1} \left(1 - \frac{j}{n}\right)$$

Let us now take the limit as $n\to\infty$ on both sides

$$\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n = 1 + \lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k!} \prod_{j=1}^{k-1} \left(1 - \frac{j}{n}\right)$$

Since $\frac{j}{n} \to 0$ when $n\to\infty$, the product term simply turns into the product of a whole bunch of $1$s. As a result, regardless of what $n$ or $k$ is, the whole product becomes $1$. Hence

$$\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n = 1 + \sum_{k=1}^\infty \frac{1}{k!}$$

Because $0!=1$, $\frac{1}{0!} = 1$. As a result, we can bring the $1$ that's in front of the summation back into the summation. Hence

$$\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n = \sum_{k=0}^\infty \frac{1}{k!}$$

QED.

I would recommend trying this for yourself, by attempting to prove that this holds true for all $e^x$. Here's a hint to get you started: $e^x = \lim\limits_{n \to 0} \left(1 + \frac{x}{n}\right)^n$

Finally, you ask the big boy. The mega question. The real thinker. What does $e^{i\theta} = \cos(\theta) + i\sin(\theta)$ mean?

There are two common approaches to this. Firstly, there is the method that uses the Taylor series of $\sin(x)$, $\cos(x)$, and $e^{ix}$. But if I'm being perfectly honest... I kinda really don't want to go through the trouble of doing all that LaTex again. Which is why we move on to the second way: the Picard-Lindelöf theorem.

This theorem states that given that there are $2$ functions which satisfy

1. The same differential equation and
2. The same initial conditions

The two functions will be equal

Let us look at the function $f(x) = e^{ix}$. The derivative of this function becomes $ie^{ix}$. Hence, this is a solution to the differential equation $f(x) = if'(x)$. In addition, let us take note of the fact that $f(0) = 1$. This will become important later.

Next, let us take a look at the function $g(x) = \cos(x) + i\sin(x)$. In this case, $g'(x) = -\sin(x) + i\cos(x) = i(\cos(x) + i\sin(x))$. Therefore, $g'(x) = ig(x)$. in addition, $g(0) = \cos(0) + i\sin(0) = 1 + 0i = 1$.

Therefore, we know that the two functions have the same initial values. We know that they both are solutions to the same differential equation. As a result, we can state (by Picard-Lindelöf) that $e^{ix} = \cos(x) + i\sin(x)$. (Please note that this is not my proof. This is something I retrieved from this video; see Epic Math Time's segment on the proof of Euler's Formula). If you have the time, feel free to attempt the other method as well. It is actually simple enough if you do it by hand, given that you expand everything out rather than leaving it in terms of sigma notation.

Now onto the more pressing question: what does this mean?

Let us begin by opening the complex plane (take the $y$ axis to be the imaginary axis and the $x$ axis to be the real axis)

Given that you have a complex number $z = a + ib$ (where $a$ and $b$ are both members of the real numbers) $a$ will be the real part of $z$, and $b$ will be the imaginary part of $z$. We can plot $z$ using rectangular coordinates.

Given $z = \cos(t) + i\sin(t)$, $\cos(t)$ is the real part of $z$, and $\sin(t)$ is the imaginary part of $z$. We can hence parameterize the real and imaginary parts of $z$ in terms of an arbitrary parameter $t$ (which, as is customary with calculus, is measured in radians). Drawing this on the graph gives us the following;

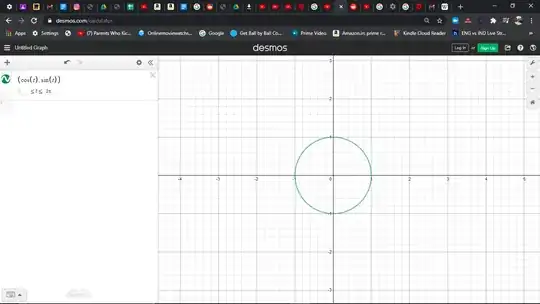
As we can see, this image shows a unit circle. So the graph of outputs of $\cos(x) + i\sin(x)$ forms a unit circle on the complex plane. But we proved earlier that $\cos(x) + i\sin(x) = e^{ix}$. Therefore, given that we have a real number input $x$, the output of the function $e^{ix}$ will be a unit circle on the imaginary plane. I just spent over an hour on just the LaTex. Please send help. Peace out.