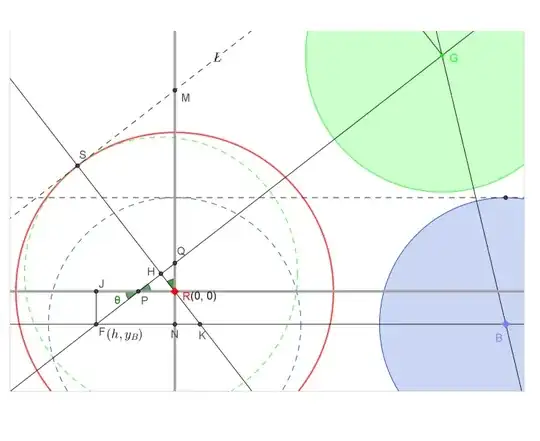
Pardon the amateurish notation and what's probably a very simple puzzle for most on this site. Still, the solution eludes me....
I have 3 circles $C_R, C_G, C_B$ as shown in the diagram. I know the $x$ and $y$ coords of each circle's center, as well as their respective radii, $r_R, r_G, r_B$.
I am looking for the formula to compute the x and y coords of the purple point F in terms of the 3 circles' x, y and r.
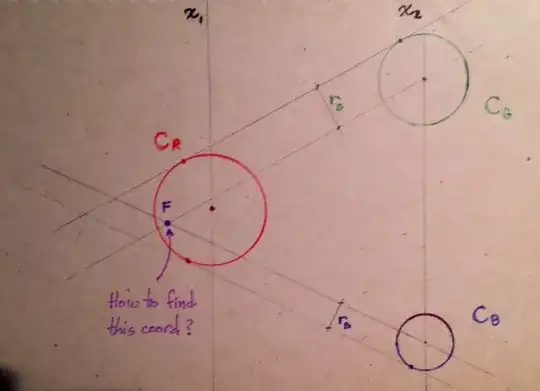
F is derived from:
- finding the tangents between 1) $C_R$ and $C_G$ and 2) $C_R$ and $C_B$,
- offsetting each tangent by 1) $r_G$ and 2) $r_B$
- computing the intersection F of the two offset lines
(A potentially simplifying assumption here is that $C_G$ and $C_B$ are horizontally aligned, ie their centers always have the same x coordinate)