I've just been studying cyclic quads in geometry at school and I'm thinking see seems pretty interesting, but where would I actually find these in the real world? They seem pretty useless to me...
-
11You may or may not know this... but your school is a part of the real world. When you learn in school, you learn for real – Ben Grossmann Jul 14 '16 at 20:09
-
2I realise that, but right now it seems as though the only use for learning cyclic quadrilaterals is so that you can come back later and teach it, just a pointless loop... – mr-matt Jul 14 '16 at 20:10
-
1In all seriousness, I would have a hard time answering this question about anything geometry related. I'm sure it's all important if you're an architect, for example. – Ben Grossmann Jul 14 '16 at 20:11
-
Suppose you have four boards, not one of which is longer than the sum of the other three lengths. Is there a geometric result you might apply to arranging the boards to box in an area? – hardmath Jul 14 '16 at 20:12
-
Fair point, though I don't see very many buildings that would relate to it! – mr-matt Jul 14 '16 at 20:12
-
@hardmath I don't understand... – mr-matt Jul 14 '16 at 20:12
-
3Well, at one time they were pretty useful, hardcore applied math even. In the Almagest, Ptolemy uses the result we now know as Ptolemy's Theorem as an aid for computing his table of chords, an important tool for astronomical calculations. – André Nicolas Jul 14 '16 at 20:12
-
8I am going to ask, when do plan to use what you learned about Shakespeare's Tragedies, Ancient History, or Chemistry "in the real world." Only in math class to people ever ask, "When am I going to use this." And you are missing the point. Yes, frequently math is useful. But you learn math to learn how to think logically -- to apply reason and rationality. – Doug M Jul 14 '16 at 20:13
-
@DougM Yes that is true, half the stuff I learn in school is utterly useless but you do have a good point there. – mr-matt Jul 14 '16 at 20:14
-
@DougM don't be too hard on him, he did say it was an interesting thing to learn about after all. To your point, however, I would say that math is one of the few classes that is marketed as "useful". A thorough discussion about this broader issue in math education, however, is neither here nor there. – Ben Grossmann Jul 14 '16 at 20:17
-
Ah, but but what you are really learning is not "useless." What is important are the processes more than the facts. How to communicate clearly, how to draw connections between apparently unrelated events to form a picture of the whole, how do conduct a controlled experiment, and how to apply logic. – Doug M Jul 14 '16 at 20:20
-
Doug M. What always bugged me was that as math described the world math was the only thing I imagined using in the real world. But on the other hand I don't feel this is the op's question. I think s/he is asking when physically do cyclic quads appear. On the third hand I think this is an odd question because if you know what cyclic quads are, you know precisely when they occur. – fleablood Jul 14 '16 at 20:20
-
@fleablood "if you know what cyclic quads are, you know precisely when they occur" Exactly, but I just can't see any cases of them occurring in the real world... – mr-matt Jul 14 '16 at 20:27
-
BTW, rectangles are cyclic quadrilaterals. – ccorn Jul 14 '16 at 20:35
-
2Um... you don't? They occur every time you inscribe something in a circle! So constructing efficient habitats in space, beehives and tectonic pressure plates, efficiency in resource allocations within city bounderies, hubcaps, steam railroad wheel ratios, architecture, trigonometry and surveying, the list is endless. – fleablood Jul 14 '16 at 20:42
-
If you build anything in which there is uniform external pressure, and by pressure I don't nescessarily mean literal physical pressure; it could be abstract such as population density and frequency in acceptible individual commute distances or location of convenience stores say. Then stability and form will reflect circular inscriptions. – fleablood Jul 14 '16 at 20:48
-
Long ago there were many similar critiques about number theory. But nowadays one doesn't need to look far to find applications, e.g. cryptography, coding theory, etc. You never know when someone will find some surprising application of "pure" mathematics. See The Unreasonable Effectiveness of Mathematics, and see here. – Bill Dubuque Jul 14 '16 at 20:51
-
If you were (will be) a mechanical engineer, you would have no doubts about the practical importance of inscribed (cyclic) and circumscribing (tangential) polygons! – G Cab Jul 14 '16 at 21:33
-
1The point of mathematics is not real-world applications. – anomaly Jul 15 '16 at 00:32
-
1@fleablood : If what you inscribe in a circle is a triangle, then how does a cyclic quadrilateral occur there? And most quadrilaterals are not cyclic. So you comment looks to me like mere assertions. $\qquad$ – Michael Hardy Jul 15 '16 at 01:07
-
@ccorn: true, but it still doesn't follow from "knowing the properties of rectangles is useful", that "knowing the properties of cyclic quadrilaterals is useful". It's easy to see that there are properties of rectangles that we use in everyday life, and those might satisfy a student that it's "worth" learning about rectangles (although one can counter-argue that a brick-layer does his job without any mathematical appreciation of theorems he's using). But the ones I can immediately think of that I commonly use are not properties of all cyclic quadrilaterals, so a better argument is needed. – Steve Jessop Jul 15 '16 at 09:36
3 Answers
I can't think of any applications, and I doubt any satisfactory ones exist - for example, as noted in the comments there may well have been connections to astronomy, but I think it's fair to suggest that almost no-one who is being taught circle theorems is going to use them in their life at any point.
Thus, I'm going to interpret this question as:
Why would you bother learning a theorem that has no application in real life?
And I think there are two good answers to this question:
1. It is interesting
This is, really, the only reason you're taught anything in your life other than how to pay taxes. Geometry is something that lots of people over a long period of time have found to be intrinsically interesting. The reasons for this are complicated - it's a good intellectual exercise, and for many people intellectual exercises are something they enjoy doing.
2. It forces you to think logically
The patterns of thought people generally use in mathematics are valuable. Logical arguments are important in all walks of life, and being able to understand and interpret them is an extremely valuable life skill which you really should want to have.
I have a lot of sympathy with this question, for the following reason: you are probably taught mathematics very badly. The arguments I give above really rely on the idea that you are taught how to prove theorems (and Euclidean geometry is a fantastic exercise in proof). Without that, I would claim that learning geometry really has no value. I would even go so far as to say you shouldn't bother going so far as to learn basic trigonometry (unless you need it to be an engineer or something), unless you study its proof. That really is where all the value, and all the fun, is.
This is not your fault. But there is something you can do about it. Look up a proof, try to understand it, and if you're lucky you'll get a little intellectual buzz from the 'aha!' moment of it all coming together. But, I'm sorry to say, you'll probably have to do this yourself. Mathematics teaching is woeful in the vast majority of schools, and statistically speaking you are unlikely to even have a teacher capable of explaining to you why these results are true, let alone interesting or useful.
So, on the off chance that this answer has spiked your curiosity, I recommend writing another question, called "How do you prove interesting facts about cyclic quadrilaterals?", and you might get a more satisfying answer.
- 17,121
-
1When I was working in math fields a while ago and my students approached me with the same question I would answer that math science is 200 years ahead from physical world. Who know what we may come across in nature but by the time discover new phenomena, we might try mathematical apparatus already available to us to describe it. Not to mention, math is abstract, it flexes your mind, teaches you critical thinking. Things like Sufficient vs. Necessary conditions are all over our lives. I find that a lot of people do not understand this. – AstroSharp Jul 14 '16 at 22:25
-
1@AstroSharp I see what you're saying, but I don't think I agree. I don't think anyone seriously does mathematics with the hope of "setting up the future". I prefer to emphasise the very real fact that maths is a good exercise in logical thinking, which is good for enriching one as a human being. – preferred_anon Jul 14 '16 at 23:15
-
@AstroSharp: all of these circle-theorems are a lot more than 200 years old though, so while your first argument might help to justify academic study of number theory (used for crypto) or higher-dimensional manifolds (used for physics), it's not relevant for 2000-ish-year-old geometry. There should be (and are) some applications of that visible by now, but the trouble comes in convincing a high-school student that those applications will occur in their personal life :-) – Steve Jessop Jul 15 '16 at 09:28
-
1That is to say, you have a great argument for persuading a funding body not to entirely abandon pure mathematics on principle, but schoolkids probably don't expect to be physicists in 200 years time! – Steve Jessop Jul 15 '16 at 09:44
-
I'm pretty sure back when my mother taught me to look left and right before crossing the street, she neither thought it was an interesting thing to learn, nor did she think about the taxes I might not be able to pay later if I didn't do it. – celtschk Jul 15 '16 at 10:28
Theorem 3 of the Bern-Eppstein paper cited below proves that any polygon of $n$ vertices may be partitioned into $O(n)$ cyclic quadrilaterals. A hint of how this might be achieved can be glimpsed in the figure below, where all the white quadrilaterals are cyclic.
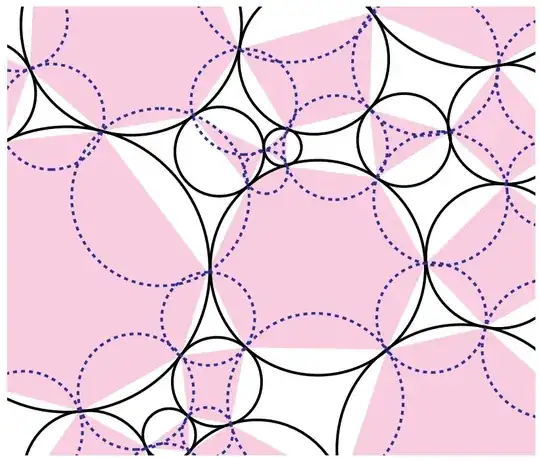
Fig.5 from cited paper.
Quadrilateral meshing is important in many applications. The cyclic quads produced by their algorithm have desirable "quality" characteristics.
Bern, Marshall, and David Eppstein. "Quadrilateral meshing by circle packing." International Journal of Computational Geometry & Applications 10.04 (2000): 347-360. (Pre-journal arXiv abstract.) (Journal link.)
- 30,327
Ptolemy's theorem says that if $a,b,c,d$ are the lengths of the sides of a cyclic quadrilateral, with $a$ opposite $c$ and $b$ opposite $d$, and $e,f$ are the diagonals, then $ac+ bd = ef$. In the second century AD, Ptolemy used that to prove identities that today we would express as \begin{align} \sin(a+b) & = \sin a \cos b + \cos a \sin b, \\ \cos(a+b) & = \cos a \cos b - \sin a \sin b. \end{align} As to where these come up in Reality, you can start with this: https://en.wikipedia.org/wiki/Uses_of_trigonometry
PS: A bit more on what Ptolemy did: https://en.wikipedia.org/wiki/Ptolemy%27s_table_of_chords