4

For the graph of $$y=\sqrt{x}\sin \frac{1}{x},$$ Do the following limits exist? If so, what is it?

(a) $\lim_{x \to 0^+} f(x)$
(b) $\lim_{x \to 0^-}f(x)$
(c) $\lim_{x \to 0}f(x)$

By the way, the graph is $\sin \frac{1}{x}$ inside of the parabola $x=y^2$

Here's what I got
(a) Yes, the limit is $0$
(b) No
(c) No

I am confused on (a) because if $x$ approaches $0$ from the right hand side, then, according to the parabola, it reaches the limit $0$. But if $x$ approaches $0$ from the right hand side, according to $\sin\frac{1}{x}$, there is not limit. Please help?

levap
  • 65,634
  • 5
  • 79
  • 122
BlueMagic1923
  • 781
  • 4
  • 11
  • 24
  • What do you mean in (a) and (b)? Your function isn't defined for $x<0$ or isn't it a real function? –  Jul 10 '16 at 18:37
  • 3
    $\sin(1/x)$ wiggles desperately back and forth, but it stays between $-1$ and $1$, so $\sqrt{x}$ drags it down to $0$. Your answers are all correct. – André Nicolas Jul 10 '16 at 18:37
  • 4
    For (a): We have $0\leq \sqrt{x}\sin(1/x)\leq \sqrt{x}$ and $\lim_{x\to 0+}\sqrt{x}=0$. So by squeeze theoreme your answer is correct. –  Jul 10 '16 at 18:38
  • Alright, thank you guys! – BlueMagic1923 Jul 10 '16 at 19:05
  • The multiple choice options are wrong. Both $a)$ and $c)$ are correct, if we take for granted that the domain of $f$ is $\mathbb{R}_{> 0}$. – MathematicsStudent1122 Jul 10 '16 at 20:19

1 Answers1

1

Well, let's look at sin ($\frac{1}{x}$) first. As x approaches 0 from either direction, $x\rightarrow 0$, so $\frac{1}{x}\rightarrow +\infty $. But by the definition of sine,|sin t| $\leq 1$ where $t\in \mathbb R$. So consider $(a,b) \subset \mathbb R $ where $0\in $(a,b). Then there will be 3 possible extreme values of y= f(x): 1) $x\in (a,b)$ such that $\frac{1}{x}=2n\pi$ where $n\in \mathbb N$.

2) $x\in (a,b)$ such that $\frac{1}{x}=2n\pi$ + $\frac{\pi}{2}$

and

3) $x\in (a,b)$ such that $\frac{1}{x}=2n\pi$ + $\frac{3\pi}{2}$

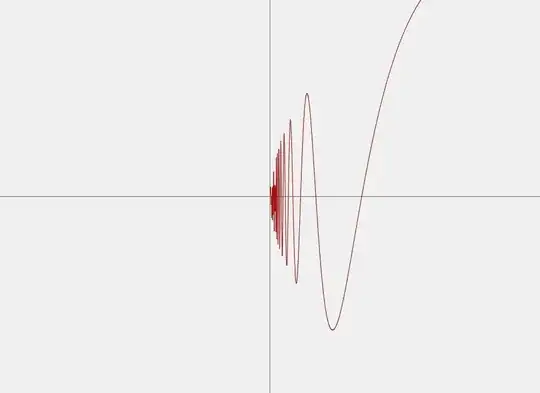
Therefore, sin ($\frac{1}{x}$) oscillates back and forth between 1 and -1 in any open neighborhood of x -> 0. Technically,due to the $\sqrt x$ term, f(x) is undefined at x < 0. But since we can approach 0 from the left and f(0) is defined, we can take the absolute value of x and obtain the same result in calculating the limit.

Now consider $\sqrt x$ sin $(\frac{1}{x})$. By the Cauchy Schwartz inequality and the result above:

| $\sqrt x$ sin $(\frac{1}{x})$| $\leq$ |$\sqrt x$||sin $(\frac{1}{x})$|$\leq$ | $\sqrt x$| < $\epsilon$ where $\epsilon$ = $\sqrt\delta$ whenever |x| < $\delta $. So $lim_{|x|\rightarrow 0}$ $\sqrt x$ sin $(\frac{1}{x})$ = 0!

Here's the graph to justify our limit visually:

enter image description here

Mathemagician1234
  • 17,288