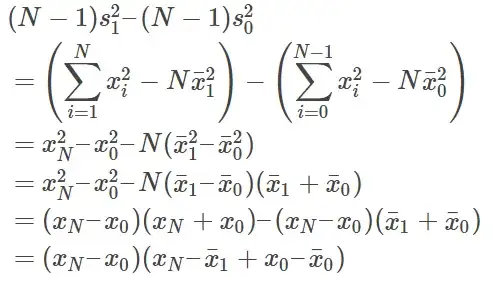Calculating variance for a window of samples which already contains pre-calculated variances

Question

In a previous answer, the following solution was given for calculating the variance from a stream of sample values (from Knuth via John D. Cook):

$$ \begin{align*} m_k&=m_{k-1}+\frac{x_k-m_{k-1}}k \\ v_k&=v_{k-1}+(x_k-m_{k-1})(x_k-m_k) \end{align*} $$

with variance $$\sigma^2=\frac{v_k}{k-1}$$

If we kept track of $m_k$, $v_k$, and $\sigma^2$ for each sample, then could we easily compute the variance for a given window of samples between $i$ and $i+j$ with a simple manipulation of those saved values?

Answer 1

Looks like an answer can be found here: http://jonisalonen.com/2014/efficient-and-accurate-rolling-standard-deviation/

If the window is moving from $$(x_0,...,x_N-_1)$$ to $$(x_1,...,x_N)$$ then: