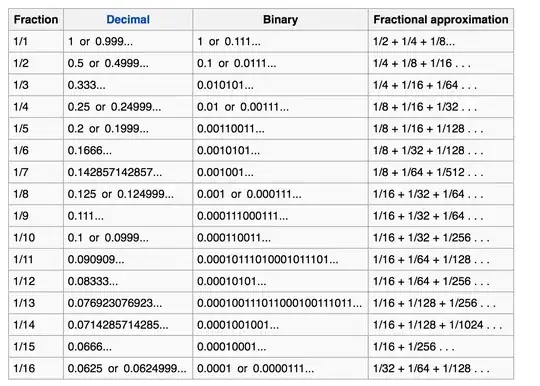
I am studying a Computer Organization course, but in the slides it is mentioned that I have to convert fraction numbers to IEEE floating point representation. To do that first, I have to convert the irrational number to fractional representation, for example here are some common fraction approximations:
In the slide, they tried to explain how the fractional approximation of 1/3 was done, but I still didn't understand it:
How do I convert 1/3 to fractional approximation? I can't seem to find any method online?