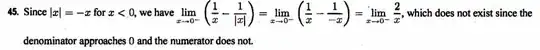I was working on a few problems from James Stewart's Calculus book (seventh edition) and I found the following:
Find
$$\lim_{x \to 0^-} \left( \frac{1}{x} - \frac{1}{|x|} \right)$$
Since there's a $|x|$ on the limit and knowing that $|x| = -x$ for any value less than zero, we have
$$\lim_{x \to 0^-} \left( \frac{1}{x} - \frac{1}{|x|} \right) = \lim_{x \to 0^-} \frac{2}{x}$$
So far so good. Continuing,
$$\lim_{x \to 0^-} \left( \frac{1}{x} - \frac{1}{|x|} \right) = \lim_{x \to 0^-} \frac{2}{x} = - \infty$$
since the denominator becomes smaller and smaller. When checking the textbook's answer I've found the following:
Am I missing something or should the limit really be $- \infty$ ?