1

I am confused about concept of "undefined " . For example the value of $f(x) = (x^2-1)/(x-1)$ at $x=1$ or $f(x) = (x^2-4)/(x+2)$ at $x=-2$ is exist ? If not why in wolfram alpha's site is exist even though for determine domain, we can see $x\not= 1$ and $x\not= -2$. https://www.wolframalpha.com/input/?i=(x%5E2-1)%2F(x-1) https://www.wolframalpha.com/input/?i=(x%5E2-4)%2F(x%2B2)

And finally, what's the difference between concept of $0/0$ and $1/0$ ?

Please Help. Thanks.

Yuriy S
  • 31,474
S.H.W
  • 4,379
  • As for your example, $f(1)=2$ which is obvious if you use $(x^2-1)=(x-1)(x+1)$ – Yuriy S Jul 03 '16 at 21:22
  • Yes , but in the plot of function is a hole at $x=1$ or it's continuous ? – S.H.W Jul 03 '16 at 21:24
  • Technically, the limit at $x \to 1$ exists and is equal to $2$ (in fact, both left and right limits are equal to $2$), so I guess it depends on how you define the function. It could have a hole. But I suggest you just use a different example to show what you mean. Preferably two examples, for two cases you want to find the difference between – Yuriy S Jul 03 '16 at 21:26
  • Okay , I will do it! – S.H.W Jul 03 '16 at 21:32
  • About the edit - your second example is exactly the same as the first example – Yuriy S Jul 03 '16 at 21:32
  • Yes , my problem is exactly here. It's better to say I have two problems. First is in that point a hole or not , and second difference between $0/0$ and $1/0$. – S.H.W Jul 03 '16 at 21:34
  • 1
    Try this (more general) case https://en.wikipedia.org/wiki/Removable_singularity – Yuriy S Jul 03 '16 at 21:35
  • Try this link as well https://en.wikipedia.org/wiki/Classification_of_discontinuities – Yuriy S Jul 03 '16 at 21:43
  • http://math.stackexchange.com/questions/125186/why-not-to-extend-the-set-of-natural-numbers-to-make-it-closed-under-division-by/125208#125208 –  Jul 04 '16 at 00:43

1 Answers1

9

Guess what, computers can lie to you.

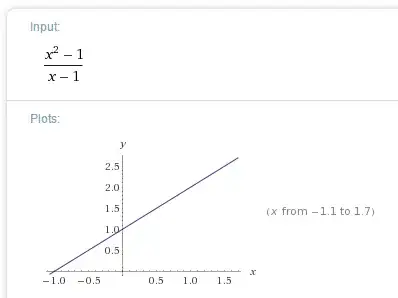
enter image description here

Hey look, f(1) = 2. We can divide by zero after all. Nope, sorry, thanks for playing.

First, understand that computer generated graphs are nothing but points strung together. What you're looking at is an attempt to correctly draw the graph. The flaw is that every pixel takes up space. So we can zoom in on that graph right where we know there should be a discontinuity and never find it because zooming might never force the computer to actually try f(1).

You can use limits to discover things that happen really close to f(1) and many other things but without throwing a limit around that function or restricting its domain it's simply not true that:

$$f(x) = \frac{x^2-1}{x-1}=\frac{(x-1)(x+1)}{x-1}=x+1,$$

This is true everywhere except where x is 1.

So why does wolframalpha make it look like it's the same?

enter image description here

Using the magic of my brain I can zoom in on the empty spot in the pixel and show you where x=1 leaves a hole in your graph (yeah that hole is not to scale, if it was we couldn't see it). If wolframalpha happened to miss testing that spot (and say, test a little less than 1, where that red dot is) then it thinks it's ok to light up that pixel because it can find a value inside it that is true.

Doesn't mean there isn't still a tiny infinitesimal hole in the graph. Infact to prove there isn't one in there wolframalpha would have to test an infinite number of x values inside that pixel to prove there isn't one there. I'm guessing you don't have that kinda time to wait for the page to load.

Keep studying limits. They teach you about these holes, what they mean, when to care about them, and when not to.

As for 1/0 vs 0/0. These are different, mostly in how they were formed. With more information about how they were formed, limits might be able to tell us interesting stories.

0/0 is an indeterminate form which just means whatever created it might have a defined limit like our function does at (1,2). If all you told me was "it's 0/0" I'd have no idea what it's limit was.

1/0 has no chance at having a limit since whatever created it has let the numerator get infinitely larger than the denominator.

But expressed without background info, only as 0/0 and 1/0, even limits aren't much help. They simplify to the same thing, undefined. They are both holes in our algebra. They are destroyers of information. Handle them with care.

candied_orange
  • 672
  • 1
    This answers the question exactly and correctly. –  Jul 03 '16 at 22:09
  • @Yuriy S Yes you are right but I think it's good information about generation of computer to plotting and I will be happy if there's more references about it. – S.H.W Jul 03 '16 at 22:15
  • @CandiedOrange Thank you for that answer. If you have any references about generation of computer to plotting , I will use that. Thanks a lot! – S.H.W Jul 03 '16 at 22:22
  • @S.H.W not 100% sure what you want but a google search for "discontinuity plotting points on a graph" turns up stuff like this. – candied_orange Jul 03 '16 at 22:51
  • '0/0 is an indeterminate form which just means whatever created it might have a defined limit like our function does at (1,2)'. Yes, like here. –  Jul 04 '16 at 00:39
  • Okay , thank you a lot! – S.H.W Jul 04 '16 at 02:28