I have learn that the exterior product is an oriented plane called bivector given as $A \times B = |A||B| \sin x (i \times j)$ For $x \in(-\pi,\pi)$. I will like someone to derive the cross product and the exterior product with a geometry picture to show the difference.
-
What are $i$ and $j$? – Hoot Jun 27 '16 at 19:14
-
@Hoot.they are unit vector(oriented line) – Wahadti Vitalis Jun 27 '16 at 19:46
-
1According to your description, the exterior product of two vectors is a bivector. But the cross product of two vectors (in 3-space) is a vector. So we need an identification of bivectors to vectors, which is easy to do given the coordinate system. – GEdgar Jun 27 '16 at 21:43
-
@WahadtiVitalis Have you seen my answer to this question? It may help a bit with the definitions. I also derived $|A\times B| = |A||B|\sin(\theta)$, and by extension $|A\wedge B| = |A||B|\sin(\theta)$. – Jun 30 '16 at 00:12
2 Answers
I don't know what you mean by derive here, but by definition the two products give different types of geometric objects. The exterior product of two vectors (in $\mathbf{R}^n$, for any $n$) is a bivector, whereas the cross product of two vectors (in $\mathbf{R}^3$ only) is another vector. For $n=3$, there happens to be an isomorphism between bivectors and vectors, and the cross product is what you get if you take the exterior product and the convert then resulting bivector to a vector using this isomorphism.
- 53,395
I believe the exterior products (wedge products) of two vectors $u$ and $v$ are denoted by $u\wedge v$. Note: the $LaTeX$ command for wedge products is also \wedge.
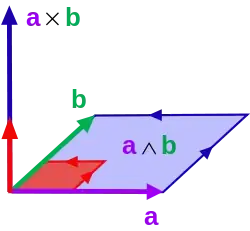
I have borrowed this picture from Wikipedia's page on exterior algebra as it explains the difference very clearly. $a\times b$ is the cross product of the two vectors $a$ and $b$. The cross product gives a vector that is perpendicular to both $\vec{a}$ and $\vec{b}$ as you can see in the diagram. This is particularly useful in physics where we encounter several cross products in nature: torque $\tau=\vec{r}\times \vec{F}$ where $\vec{r}$ is the radius from the axis of rotation and $\vec{F}$ is the force, force on a moving charge $\vec{F}=q\vec{v}\times\vec{B}$ where $\vec{B}$ is the magnetic field, and so on.
Thus, this led to the "right-hand rule as we want to find the direction of the vector cross product. Note: in the picture, even a vector anti-parallel to the vector $a\times b$ would be perpendicular to both vectors $a$ and $b$.
Imagine: $\vec{a}$ as your thumb and point your thumb in the direction of $\vec{a}$. $\vec{b}$ as your fingers and point them in the direction of $\vec{b}$. $\vec{a}\times \vec{b}$ is in the direction that your palm is pointing.
On the other hand, the wedge product is used to determine areas, volumes, etc, as shown by $a\wedge b$, which shows the area of a parallelogram. This is exactly the formula that you have provided us as it determines the area of the parallelogram from two vectors $\vec{A}$, $\vec{B}$, and the angle between $\vec{A}$ and $\vec{B}$.
Note: the magnitude of the cross product as shown below also gives the area of a parallelogram. Of course, this is different from taking only the cross product itself as we have the magnitude (length of a vector) here instead. $$||a\times b||=||a||\quad\!\!\!||b||\quad\!\!\!|\sin\theta|$$
- 178
-
@Brittany.thanks for your answer.But my other problem is a clean derivation of the two product because I have seen in some textbooks that – Wahadti Vitalis Jun 27 '16 at 19:55
-
Sinx appears in the cross product and the wedge product and I didn't see how that come about... – Wahadti Vitalis Jun 27 '16 at 20:01
-
I have edited my comment. You can see the changes at the end. I think you were referring to the magnitude of the cross product for the appearance of $\sin$ – Melinda Jun 27 '16 at 20:19
-
Great!!.how can I derive a×b=|a||b|sinx(i×j) for "×" as cross product. And how can I derive a ^ b = |a||b|sinx(i^j) for "^" a wedge product.sorry to disturb you because I have try to derive this equation knowing what intuitively what this products mean. – Wahadti Vitalis Jun 27 '16 at 20:39
-
By definition, $||a\times b||^2=||a||^2||b||^2-(a\cdot b)^2=||a||^2||b||^2(1-\cos^2\theta)\rightarrow ||a\times b||=||a||||b|| |\sin\theta|$ – Melinda Jun 28 '16 at 02:16
-
@Brittany Just a note: I actually think that torque and the magnetic force are better described by bivectors than (pseudo)vectors. – Jun 30 '16 at 00:07