-1

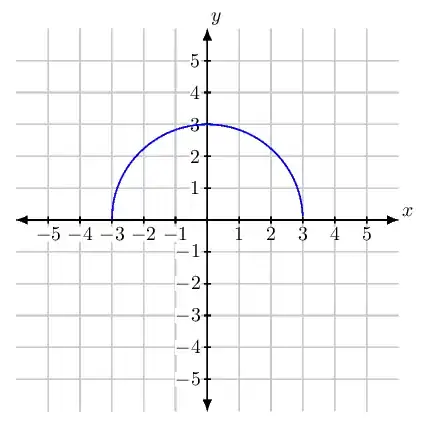
What is the domain and range of real function $f(x) = \sqrt{9 − x^2}$?

In order to find the function's domain, you need to take into account the fact that, for real numbers, you can only take the square root of a positive number. In other words, in order for the function to be defined, you need the expression that's under the square root to be positive. \begin{align*} 9−x^2 & \geq 0\\ x^2 & \leq 9\\ |x| & \leq 3 \end{align*} This means that you have $x \geq −3$ and $x \leq 3$.

Therefore, the domain of the function will be $x \in [−3,3]$.

But what will be the range?

Help appreciated!

N. F. Taussig
  • 76,571
Cyril Cherian
  • 101
  • 1
  • 4
  • 3
    Have you tried drawing a graph? – hmakholm left over Monica Jun 25 '16 at 11:43
  • 3
    Hint: $y=\sqrt{9-x^2}\implies x^2+y^2=9$. –  Jun 25 '16 at 11:45
  • so is this a circle with radius 3 ? – Cyril Cherian Jun 25 '16 at 11:47
  • Not quite. Notice that $f(x)$ can't be negative. –  Jun 25 '16 at 11:47
  • So the range will be [-3,3] why cant f(x) be negative? – Cyril Cherian Jun 25 '16 at 11:48
  • No, the graph of $x^2+ y^2= 9$ is a circle. For your original function, $y= \sqrt{9- x^2}$, y is non-negative. Its graph is the upper half of that circle. – user247327 Jun 25 '16 at 11:48
  • 1
    Clearly $y\geq 0$. Now we find whether the function is increasing or decreasing by finding first derivative and second derivative $y^{\prime},y^{\prime \prime}$. Clearly $y^{\prime \prime} \geq 0$, hence the function is decreasing. Function attains maximum value at $x=0$ and minimum at $x=3,-3$. Hence the range is $[0,3]$ – Shahid M Shah Jun 25 '16 at 11:49
  • $f(x)$ can't be negative because you can only take the square root of nonnegative numbers, and the square root of a nonnegative number is nonnegative. To convince yourself of that try to find an $x$ in $[-3,3]$ (or in fact in any domain) such that $f(x) = -3$. –  Jun 25 '16 at 11:50
  • Ok Shahid @x = 0 is'nt the function going to SQRT(9) = +3 or -3 why [0,3] ? – Cyril Cherian Jun 25 '16 at 11:50
  • 1
    Then this will be relation not function! If you define relation as function then we take only principal root. – Shahid M Shah Jun 25 '16 at 11:51
  • Why are we taking principal root here? why not consider the -ve 3 this is not clear – Cyril Cherian Jun 25 '16 at 11:55
  • No: $\sqrt{9}=3$, not $-3$ (in high school at least). See this answer. –  Jun 25 '16 at 11:55
  • Ok what about above high school in that case will this be range= [-3,3] – Cyril Cherian Jun 25 '16 at 11:59
  • You can define $\sqrt{}$ as a relation rather than a function -- meaning it can take multiple values for a single input. But even beyond high school this is not very desirable most of the time. So for real numbers at least, defining $\sqrt{}$ as a function by having it return only the principal (meaning nonnegative) square root is the usual convention. –  Jun 25 '16 at 12:01
  • 1
    If you're convinced that your teacher defines $\sqrt{}$ as a multivalued relation, then you're right: the range will be $[-3,3]$. But I think that is unlikely. -- Especially since the notation $f(x)$ is almost exclusively used for functions, not relations. –  Jun 25 '16 at 12:04

5 Answers5

1

Hint:

Since a square is non-negative, $0\le 9-x^2\le9\;$ on $\;[-3,3]$, and $\;\sqrt x\;$ is a continuous increasing function.

Bernard
  • 175,478
1

You correctly found the domain, although you meant that the expression that's under the square root, which is called the radicand, must be non-negative.

Observe that $y = \sqrt{9 - x^2} \implies y \geq 0$. Moreover, if we square both sides of the equation, we obtain $y^2 = 9 - x^2$, which is equivalent to $$x^2 + y^2 = 9$$ This is the equation of a circle with radius $3$ and center at the origin. The restriction $y \geq 0$ means that we obtain the upper semi-circle, from which you can determine that the range is $[0, 3]$.

upper_semi-circle

Addendum: I gather from the comments that you have left that you were not aware that the notation $y = \sqrt{x}$ means the principal (non-negative) square root of $x$. That is what allows us to conclude that $y \geq 0$.

Community
  • 1
N. F. Taussig
  • 76,571
1

The usual convention is that the principal square root function $f(x) = \sqrt x$ returns only the non-negative root. So in this case, the range corresponds to the semicircular upper half of the circle defined by $x^2 + y^2 = 9$. Which gives the range as $[0,3]$.

Deepak
  • 26,801
1

$$9-x^2\ge 0\implies D_f=[-3,3]$$ set $x=3\sin\theta$ $$y=\sqrt{9-9\sin^2\theta}=3\,|\,\cos\theta\,|\implies R_f=[0,3]$$

Behrouz Maleki
  • 11,182
1

You just need to find the absolute maxima or minima of $f(x)$ in its domain $[-3,3]$. Write $f(x)=√g(x)$, where $g(x)=9-x^2$. Now, $g(x)$ has an extrema if $g'(x)=0$ which gives $x=0$ as the point of maxima as $g''(0)<0$. Hence $f(0)=√g(0)=3$, $f(-3)=f(3)=0$. Clearly, $Range(f)=[0,3]$.

Nitin Uniyal
  • 7,946